题目内容
1. 已知:如图,在△ABC中,D为BC上的一点,连接AD,过点A作AE∥BC,且AE=DC,∠E=∠B.求证:AB=AC.
已知:如图,在△ABC中,D为BC上的一点,连接AD,过点A作AE∥BC,且AE=DC,∠E=∠B.求证:AB=AC.
分析 根据两直线平行,内错角相等可得∠ADC=∠DAE,然后利用“边角边”证明△ACD和△DEA全等,根据全等三角形对应角相等可得∠C=∠E,再求出∠B=∠C,然后根据等角对等边证明即可.
解答 证明:∵AE∥BC,
∴∠ADC=∠DAE,
在△ACD和△DEA中,$\left\{\begin{array}{l}{AE=DC}\\{∠ADC=∠DAE}\\{AD=DA}\end{array}\right.$,
∴∠C=∠E,
又∵∠E=∠B,
∴∠B=∠C,
∴AB=AC.
点评 本题考查了全等三角形的判定与性质,平行线的性质,等角对等边的性质,熟记各性质并准确识图确定出全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.两个有理数a与b,a+b=0,a与b的关系是( )
| A. | 一正一负 | B. | 互为倒数 | C. | 互为相反数 | D. | 都是零 |
11.如图所示,属于柱体的一组是( )
| A. |  | B. |  | C. |  | D. |  |
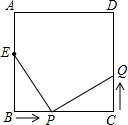 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,
 如图,FD∥BE,则∠1+∠2-∠A=180°.
如图,FD∥BE,则∠1+∠2-∠A=180°.