题目内容
两圆半径分别是r1、r2的圆心距为d，若r1-r2＜d＜r1+r2，则两圆的位置关系是（ ）
| A、相离 | B、相交 | C、外切 | D、内切 |
考点：圆与圆的位置关系
专题：
分析：根据两圆相交，则圆心距大于两圆半径之差，而小于两圆半径之和直接写出选项即可．
解答：解：∵两圆半径分别是r1、r2的圆心距为d，若r1-r2＜d＜r1+r2，
∴两圆相交，
故选B．
∴两圆相交，
故选B．
点评：此题考查了两圆的位置关系与数量之间的联系：两圆相交，则圆心距大于两圆半径之差，而小于两圆半径之和．
练习册系列答案
相关题目
一个正方形的面积是13，估计它的边长大小在（ ）
| A、2与3之间 |
| B、3与4之间 |
| C、4与5之间 |
| D、5与6之间 |
如图，已知AB∥CD，BC平分∠ABE，∠C=35°，则∠BED的度数是（ ）| A、70° | B、68° |
| C、60° | D、72° |
已知，菱形的一条对角线与一条边的和是22，和这条边的差是2，若两对角线的长都是整数，则菱形的面积为（ ）
| A、96 | B、64 | C、60 | D、48 |
下列各式，正确的是（ ）
| A、-2≥1 | ||||
| B、-3≥-2 | ||||
C、
| ||||
D、
|
如果a＞b，那么结论中错误的是（ ）
| A、a-4＞b-4 | ||||
| B、4a＞4b | ||||
C、
| ||||
| D、-a＞-b |
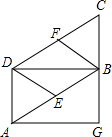已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点．
某市对九年级学生进行了一次学业水平测试，成绩评定分A、B、C、D四个等第．为了解这次数学测试成绩情况，相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析，相应数据的统计图表如下：