题目内容
8. 如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,请你猜想图中哪两条线段之和等于第三条线段,并证明你的猜想的正确性(证明你的猜想需要用题中所有的条件).
如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,请你猜想图中哪两条线段之和等于第三条线段,并证明你的猜想的正确性(证明你的猜想需要用题中所有的条件).
分析 过点D作DE⊥BC,可证明△ABD≌△EBD,则∠A=∠E=90°,利用角与角之间的关系,证得ED=EC,则可得出结论AB+AD=BC.
解答 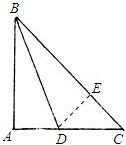 解:AB+AD=BC,证明如下:
解:AB+AD=BC,证明如下:
过点D作DE⊥BC,垂足为E,
∵BD平分∠ABC,
∴DA=DE,∠ABD=∠EBD(角平分线上的任一点到角的两条边的距离相等),
在△ABD与△BDE中,$\left\{\begin{array}{l}{AD=DE}\\{∠ABD=∠DBE}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△EBD,
∴AB=BE,
∴∠A=∠BED=90°,
∵AB=AC,
∴∠B=∠C=45°.
在△DEC中,∠DEC=90°,∠C=45°,
∴∠EDC=45°,
∴ED=EC,
∴AD=EC,
∴BE+EC=AB+AD=BC.
点评 本题考查了角平分线的性质,全等三角形的判定和性质,通过作辅助线构成全等三角形是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
18.下列各式中:$\frac{b}{2a}$;2a+b;$-\frac{x+1}{4-x}$;$\frac{1}{2}$xy+x2y;$\frac{x-y}{5}$;$\frac{5}{π}$,分式的个数( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
17.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (-a3)2=-a6 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | -22-3=-7 |
18.在△ABC中,AB=AC,∠B的外角=100゜,那么∠A=( )
| A. | 10゜ | B. | 20゜ | C. | 60゜ | D. | 80゜ |