题目内容
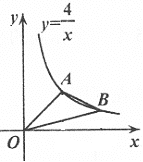
【题目】在平面直角坐标系中,己知O为坐标原点,点![]() ,以点A为旋转中心,把
,以点A为旋转中心,把![]() 顺时针旋转,得
顺时针旋转,得![]() .
.

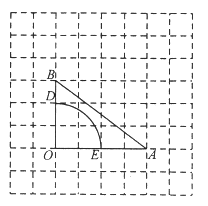
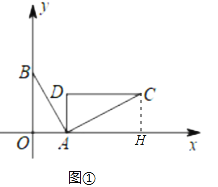
(Ⅰ)如图①,当旋转后满足![]() 轴时,求点C的坐标.
轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
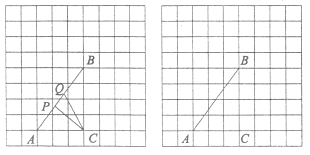
(Ⅲ)在(Ⅱ)的条件下,边![]() 上的一点P旋转后的对应点为
上的一点P旋转后的对应点为![]() ,当
,当![]() 取得最小值时,求点P的坐标(直接写出结果即可)
取得最小值时,求点P的坐标(直接写出结果即可)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)点P坐标
;(Ⅲ)点P坐标![]() .
.
【解析】
(Ⅰ)如图①中,作CH⊥x轴于H.根据旋转的性质和三个角是直角的四边形是矩形得出四边形ADCH是矩形,利用矩形的性质即可解决问题;
(Ⅱ)如图②中,作DK⊥AC于K.在Rt△ADC中,求出DK、AK即可解决问题;
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.由题意PA=AP′,推出AP′+PD=PA+PD,根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.只要求出直线A′D的解析式即可解决问题;
解:(Ⅰ)如图①中,作![]() 轴于H.
轴于H.
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
∴![]()
(Ⅱ)如图②中,作![]() 于K.
于K.

在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴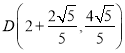
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
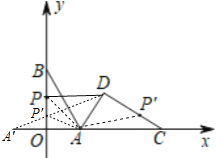
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
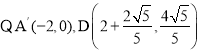 ,
,
∴直线A′D的解析式为![]() ,
,
点P坐标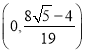

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目