题目内容
14.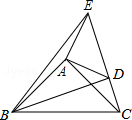 如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE=AD+AB,
其中结论正确的结论是①②③(填序号).
分析 ①由条件证明△ABD≌△ACE,就可以得到结论;
②由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°而得出结论;
③由条件知∠ABC=∠ABD+∠DBC=45°,由∠DBC+∠ACE=90°,就可以得出结论;
④根据三角形两边之和大于第三边,即可解答.
解答 解:①∵∠BAC=∠DAE,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AD=AE}\\{∠BAD=∠CAE}\\{AB=AC}\end{array}\right.$
∴△ABD≌△ACE(SAS),
∴BD=CE.故①正确;
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠CAB=90°,
∴∠ABD+∠DBC+∠ACB=90°,
∴∠DBC+∠ACE+∠ACB=90°,
∴∠BDC=180°-90°=90°.
∴BD⊥CE;故②正确;
③∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ABD+∠DBC=45°.
∴∠ACE+∠DBC=45°,故③正确;
④在△ABE中,根据两边之和大于第三边,可得BE>AB+AE,
∵AD=AE,
∴BE>AB+AD,
故④错误.
故答案为:①②③.
点评 本题考查了全等三角形的性质和判定的应用,垂直的性质和判定的应用,等腰直角三角形的性质的应用,勾股定理的应用,能利用全等三角形的性质和判定求解是解此题的关键.

练习册系列答案
相关题目
5.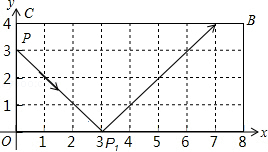 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )| A. | (1,4) | B. | (3,0) | C. | (7,4) | D. | (5,0) |
9.若M(1-3x2)=1-9x4,则M等于( )
| A. | 1-3x2 | B. | (1-3x2)2 | C. | 1+3x2 | D. | (1+3x2)2 |
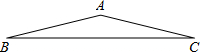 如图,△ABC中,AB=AC=2,∠B=15°,求等腰△ABC腰上高的值.
如图,△ABC中,AB=AC=2,∠B=15°,求等腰△ABC腰上高的值.