题目内容
3.求|x-1|-|x+3|的最大值与最小值,并求此时x的取值范围.分析 要求原代数式的最小值,需化去绝对值,只需对x的取值进行分类讨论,就可解决问题.
解答 解:∵当-3≤x≤1时,原式=-x+1-3-x=-2x-2,
当x≥1时,原式=x-1-x-3=-4,
当x≤-3时,原式=-x+1+x+3=4,
∴当x≤-3时,有最大值4,当x≥1时,有最小值为-4.
点评 本题考查了绝对值的化简、不等式的性质等知识,还考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
7.若函数y=ax2(a≠0)的图象与直线y=2x-3交于点(3,3b),则a,b的值分别是( )
| A. | 1,$\frac{1}{3}$ | B. | $\frac{1}{3}$,-1 | C. | -1,$\frac{1}{3}$ | D. | $\frac{1}{3}$,1 |
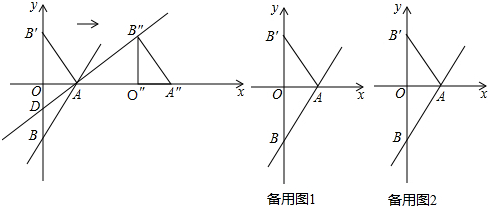
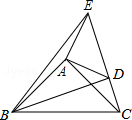 如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论: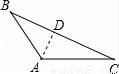 B.
B. 
 D.
D.