题目内容
14.在⊙O中,已知半径长为5,弦AB长为6,那么圆心O到AB的距离为4.分析 作OC⊥AB于C,连结OA,根据垂径定理得到AC=BC=$\frac{1}{2}$AB=3,然后在Rt△AOC中利用勾股定理计算OC即可.
解答 解: 作OC⊥AB于C,连结OA,如图,
作OC⊥AB于C,连结OA,如图,
∵OC⊥AB,
∴AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
在Rt△AOC中,OA=5,
∴OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
即圆心O到AB的距离为4.
故答案为:4.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.在数轴上,原点左边的点表示的数是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
2.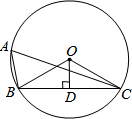 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
9.若⊙O1与⊙O2相交于两点,且圆心距O1O2=5cm,则下列哪一选项中的长度可能为此两圆的半径?( )
| A. | 1cm、2cm | B. | 2cm、3cm | C. | 10cm、15cm | D. | 2cm、5cm |
6.在以下四张图片中任意抽取一张,抽到的图片是轴对称图形的有( )个.


| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.
如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.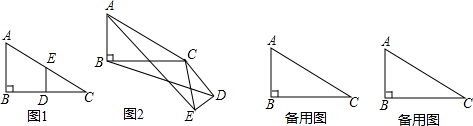
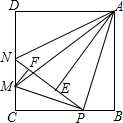 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①②⑤(写出所有正确结论的序号)
如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①②⑤(写出所有正确结论的序号)