题目内容
19.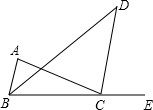 如图,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上.
如图,已知∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上.(1)试说明CD∥AB的理由;
(2)CD是∠ACE的角平分线吗?为什么?
分析 (1)由角平分线的性质得出∠ABD=∠DBC,由已知条件∠DBC=∠D,得出∠ABD=∠D,由平行线的判定方法即可得出CD∥AB;
(2)由平行线的性质得出∠DCE=∠ABC,∠ACD=∠A,由已知条件∠A=∠ABC,得出∠ACD=∠DCE即可.
解答 (1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠DBC=∠D,
∴∠ABD=∠D,
∴CD∥AB;
(2)解:CD是∠ACE的角平分线;理由如下:
∵CD∥AB,
∴∠DCE=∠ABC,∠ACD=∠A,
∵∠A=∠ABC,
∴∠ACD=∠DCE,
∴CD是∠ACE的角平分线.
点评 本题考查了平行线的判定与性质、角平分线的定义;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
9.已知点P(-3,4),则点P到x轴的距离和到y轴的距离分别为( )
| A. | 3,4 | B. | -3,4 | C. | 4,3 | D. | 4,-3 |
7. 如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )
如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )
 如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )
如图,AB∥CD,∠C=42°,∠E=58°,则∠B的度数为( )| A. | 120° | B. | 128° | C. | 80° | D. | 100° |
14. 已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )
已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )
 已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )
已知关于x的不等式x+a≤1的解集是如图所示,则a的值为( )| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
8. 将一正方体纸盒沿下图所示的线剪开,则展开图的形状为( )
将一正方体纸盒沿下图所示的线剪开,则展开图的形状为( )
 将一正方体纸盒沿下图所示的线剪开,则展开图的形状为( )
将一正方体纸盒沿下图所示的线剪开,则展开图的形状为( )| A. |  | B. |  | C. |  | D. |  |
 数学应用:
数学应用: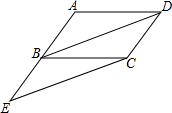 已知:如图,在?ABCD中,延长AB到E,使得BE=AB,连接BD、CE.
已知:如图,在?ABCD中,延长AB到E,使得BE=AB,连接BD、CE.