题目内容
12．计算（1）-12016-（π-3）0 （2）a5•a4+（-2a3）3
（3）2x•（x-3y）2 （4）（x-y-3）（x+y-3）
分析 （1）根据乘方运算法则、零次幂计算可得；
（2）根据同底数幂相乘、积的乘方、幂的乘方分别计算乘法和乘方，再合并可得；
（3）先根据公式计算完全平方式，再用乘法分配律去括号即可；
（4）先运用平方差公式、再运用完全平方公式计算即可．
解答 解：（1）原式=-1-1=-2；
（2）原式=a9+（-8a9）=-7a9；
（3）原式=2x•（x2-6xy+9y2）=2x3-12x2y+18xy2；
（4）原式=（x-3）2-y2=x2-6x+9-y．
点评 本题主要考查整式的混合运算，熟练掌握整式的运算法则和平方差公式、完全平方公式是解题根本和关键．
练习册系列答案
相关题目
20．某校数学兴趣小组成员小华对本班上学期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，请你根据图表提供的信息，解答下列问题：
（1）表中a=0.32，b=4，c=50，d=1；
（2）根据学校规定将有40%的学生参加校级数学冬令营活动，试确定参赛学生的最低资格线？
（3）数学老师准备从不低于90分的学生中选2人介绍学习经验，其中符合条件的小华、小丽同时被选中的概率是多少？
| 分组 | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 | 合计 |
| 频数 | 2 | 8 | 20 | 16 | b | c |
| 频率 | 0.04 | 0.16 | 0.40 | a | 0.08 | d |
（2）根据学校规定将有40%的学生参加校级数学冬令营活动，试确定参赛学生的最低资格线？
（3）数学老师准备从不低于90分的学生中选2人介绍学习经验，其中符合条件的小华、小丽同时被选中的概率是多少？
7．若一个多边形的内角和等于1620°，则这个多边形的边数为（ ）
| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
如图，在平面直角坐标系中，抛物线y=-x2+bx+c与x轴交于A（-3，0）、B（1，0）两点，与y轴交于点C，D是抛物线的顶点，E是对称轴与x轴的交点．
3．
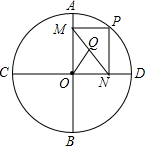如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，线段OQ所扫过过的面积为（ ）
如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，线段OQ所扫过过的面积为（ ）| A． | $\frac{π}{12}$ | B． | $\frac{π}{8}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{4}$ |