题目内容
16. 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,D是抛物线的顶点,E是对称轴与x轴的交点.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,D是抛物线的顶点,E是对称轴与x轴的交点.(1)求抛物线的解析式,并在-4≤x≤2范围内画出此抛物线的草图;
(2)若点F和点D关于x轴对称,点P是x轴上的一个动点,过点P作PQ∥OF交抛物线于点Q,是否存在以点O、F、P、Q为顶点的平行四边形?若存在,求出点P坐标;若不存在,请说明理由.
分析 (1)用待定系数法求出抛物线解析式,再利用求顶点坐标的公式即可;
(2)由条件确定出Q点纵坐标的绝对值,再分情况解一元二次方程即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}-9-3b+c=0\\-1+b+c=0.\end{array}\right.$
解得:$\left\{\begin{array}{l}a=-1\\ b=-2.\end{array}\right.$,
∴解析式为y=-x2-2x+3.
当x=-$\frac{b}{2a}$=-1时,y=4,
∴顶点D的坐标为(-1,4),
∴点F的坐标为(-1,-4).
此抛物线的草图如图所示 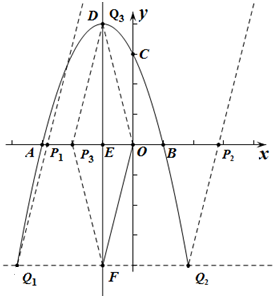
(2)若以O、F、P、Q为顶点的平行四边形存在,
则点Q(x,y)必须满足|y|=|EF|=4.
①当y=-4时,-x2-2x+3=-4,
解得,x=-1±2$\sqrt{2}$,
∴Q1(-1-2$\sqrt{2}$,-4),Q2(-1+2$\sqrt{2}$,-4)
∴P1(-2$\sqrt{2}$,0),P2(2$\sqrt{2}$,0).
②当y=4时,-x2-2x+3=4,
解得,x=-1,
∴Q3(-1,4),
∴P3(-2,0),
综上所述,符合条件的点有三个即:
P1(-2$\sqrt{2}$,0),P2(2$\sqrt{2}$,0),P3(-2,0).
点评 此题是二次函数综合题,主要考查待定系数法、数形结合、转化、分类讨论的思想方法,以及运算求解能力,画出满足条件的图形式解本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.分式$\frac{1}{xy}$,-$\frac{y}{4{x}^{3}}$,$\frac{3x}{2{x}^{2}y}$的最简公分母是( )
| A. | x2y | B. | 2x3y | C. | 4x2y | D. | 4x3y |
1.某种品牌手机经过二、三月份再次降价,每部售价由1000元降到810元,则平均每月降价的百分率为( )
| A. | 20% | B. | 11% | C. | 10% | D. | 9.5% |
8.某地气象局预报称:明天A地区降水概率为80%,这句话指的是( )
| A. | 明天A地区80%的时间都下雨 | B. | 明天A地区的降雨量是同期的80% | ||
| C. | 明天A地区80%的地方都下雨 | D. | 明天A地区下雨的可能性是80% |
 如图,折叠宽度相等的长方形纸条,若∠1=55°,则∠2=70°.
如图,折叠宽度相等的长方形纸条,若∠1=55°,则∠2=70°.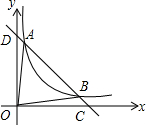 如图,直线y=-x向上平移m个单位长度得到直线l,已知直线l与双曲线y=$\frac{k}{x}$(x>0)交于A,B两点,与x轴,y轴交于点C,点D,其中点A坐标为(1,6)
如图,直线y=-x向上平移m个单位长度得到直线l,已知直线l与双曲线y=$\frac{k}{x}$(x>0)交于A,B两点,与x轴,y轴交于点C,点D,其中点A坐标为(1,6)