题目内容
如图，⊙O是以数轴原点O为圆心，半径为3的圆，与坐标轴的正半轴分别交于A、C两点，OB平分∠AOC，点P在数轴上运动，过点P且与OB平行的直线与⊙O有公共点，则线段OP的取值范围是 ．
0＜OP≤3
【考点】直线与圆的位置关系；坐标与图形性质．
【分析】点P与⊙O相切时，OP取得极值，作出切线，利用切线的性质求解即可．
【解答】解：将OA平移至P'D的位置，使P'D与圆相切，
连接OD，由题意得，OD=3，∠DOP'=45°，∠ODP'=90°，
故可得OP'=3，即OP的极大值为3
，
故答案为：0＜OP≤3．
【点评】本题考查了直线与圆的位置关系问题．关键是通过平移，确定直线与圆相切的情况，求出此时OP的值．
练习册系列答案
相关题目
C．
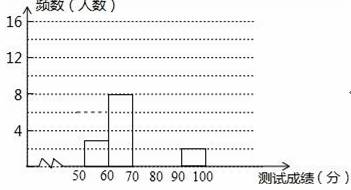
+2的值是在（ ）为了增强学生法律意识，某校举办了首届“法律进校园，法在我心中”知识大赛，经选拔后有25名学生参加决赛，这25名学生同时解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
| 组别 | 成绩x分 | 频数（人数） |
| 第1组 | 50≤x＜60 | 3 |
| 第2组 | 60≤x＜70 | 7 |
| 第3组 | 70≤x＜80 | 10 |
| 第4组 | 80≤x＜90 | m |
| 第5组 | 90≤x＜100 | 2 |
（1）求表中m的值；
（2）请把频数分布直方图补充完整；
（3）第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导，则第4组的小王与小李能同时抽到的概率是多少？
的解；