Question

若正比例函数y₁=﹣x的图象与一次函数y₂=x+m的图象交于点A，且点A的横坐标为﹣1．

（1）求该一次函数的解析式；

（2）直接写出方程组的解；

（3）在一次函数y₂=x+m的图象上求点B，使△AOB（O为坐标原点）的面积为2．

Answer 1

【考点】待定系数法求一次函数解析式．

【分析】（1）先将x=﹣1代入y=﹣x，求出y的值，得到点A坐标，再将点A坐标代入y=x+m，利用待定系数法可得一次函数的解析式；

（2）方程组的解就是正比例函数y=﹣x的图象与一次函数y=x+m的交点，根据交点坐标即可写出方程组的解；

（3）根据三角形的面积公式解答即可．

【解答】解：（1）将x=﹣1代入y=﹣x，得y=1，

则点A坐标为（﹣1，1）．

将A（﹣1，1）代入y=x+m，得﹣1+m=1，

解得m=2，

所以一次函数的解析式为y=x+2；

（2）方程组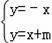的解为；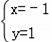

（3）设直线直线y=x+2与y轴的交点为C，与x轴的交点为D，则C（0，2），D（﹣2，0），

∵A（﹣1，1），

∴S_△AOC=S_△AOD=×2×1=1，

①当B点在第一象限时，则S_△BOC=1，

设B的横坐标为m，

∴S_△BOC=×2×m=1，解得m=1，

∴B（1，3）；

②当B点在第三象限时，则S_△BOD=1，

设B的纵坐标为n，

∴S_△BOD=×2×（﹣n）=1，解得n=﹣1，

∴B（﹣3，﹣1）．

综上，B的坐标为（1，3）或（﹣3，﹣1）．

【点评】本题考查了待定系数法求一次函数的解析式，方程组和函数的关系，三角形的面积等，分类讨论思想的运用是本题的关键．