题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上.
上.
(1)若点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)连接![]() ,若点
,若点![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .若
.若![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)点![]() 的坐标是
的坐标是![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)把点C的坐标代入直线y=x求得a的值;
(2)如图1,过点C作CE⊥y轴,垂足为点E,构造直角△BEC,利用勾股定理求得BE的长度,然后由BE=BO-OE列出关于t的方程,通过解方程得到答案;
(3)点D的坐标为(m,m),AM=n.推知Rt△OMD是等腰直角三角形,故DM=AM-AD,即m=n-![]()
①如图2,当点C在点D左侧时,过点B,点C分别作BE⊥AM,CF⊥AM,垂足分别为点E,点F,构造全等三角形:△ABE≌△CAF.结合该全等三角形的性质知DF=BE-AD=m-![]() .在Rt△DCF中,利用勾股定理求得CD=
.在Rt△DCF中,利用勾股定理求得CD=![]() =
=![]() ,根据题意列出不等式并解答;
,根据题意列出不等式并解答;
②如图3,当点C在点D右侧时,同理可求,DF=m+![]() ,CD=
,CD=![]() m+2,由1≤CD≤2,得到不等式并解答.
m+2,由1≤CD≤2,得到不等式并解答.
(1)把![]() 代入
代入![]() ,得
,得
![]() ,
,
解得![]() .
.
所以点![]() 的坐标是
的坐标是![]() .
.
(2)点![]() 在直线
在直线![]() 上,不妨设点
上,不妨设点![]() 的坐标为
的坐标为![]() .
.
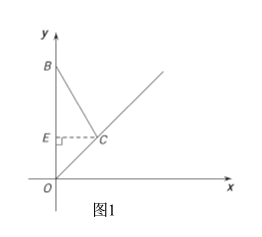
如图1,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,且点
,且点![]() ,
,
∴![]() ,
,
![]()
解得![]() .
.
∴![]() .
.
(3)∵![]() ,
,![]() ,且
,且![]() ,
,
∴点![]() 在直线
在直线![]() 上方.
上方.
∵![]() 轴于点
轴于点![]() ,
,
且![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
如图2,当点![]() 在点
在点![]() 左侧时,
左侧时,
过点![]() ,点
,点![]() 分别作
分别作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() ,点
,点![]() ,
,
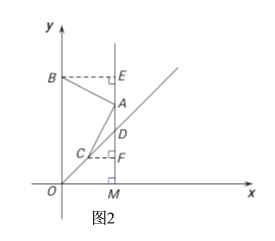
∴![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 中,
中,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,且
,且![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() .
.
∵![]() ,即
,即![]() ,
,
∴![]() .
.
如图3,当点![]() 在点
在点![]() 右侧时,
右侧时,
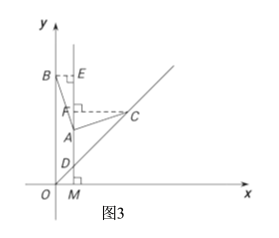
同理可求,![]() ,
,![]() ,
,
由![]() ,
,
求得![]() ,不符合题意.
,不符合题意.
综上,![]() .
.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】为了解宣城市市民“绿色出行”方式的情况,我校数学兴趣小组以问卷调查的形式,随机调查了宣城市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 |
|
|
|
|
|
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
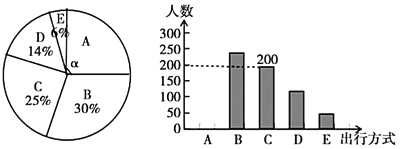
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择![]() 类的人数有______人;
类的人数有______人;
(2)在扇形统计图中,求![]() 类对应扇形圆心角
类对应扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)宣城市约有人口280万人,若将![]() 、
、![]() 、
、![]() 这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.

