题目内容
7.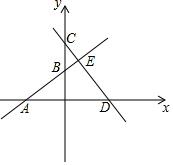 如图,一次函数y=kx+b的图象交x轴于点A(-3,0),交y轴于点B,交直线CD于E,且点C的坐标为(0,4),点D的坐标为(4,0),AB:BE=3:1,求k、b的值.
如图,一次函数y=kx+b的图象交x轴于点A(-3,0),交y轴于点B,交直线CD于E,且点C的坐标为(0,4),点D的坐标为(4,0),AB:BE=3:1,求k、b的值.
分析 过E作EF⊥x轴于F,根据平行线分线段成比例定理求得E的横坐标为1,由待定系数法求出直线CD的解析式为,进而得到E坐标,最后再由待定系数法求得结论.
解答 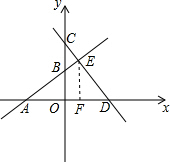 解:过E作EF⊥x轴于F,则EF∥OC,
解:过E作EF⊥x轴于F,则EF∥OC,
∴$\frac{AO}{OF}$=$\frac{AB}{BE}$=$\frac{3}{1}$,
∵A(-3,0),
∴OA=3,
∴OF=1,
∴E的横坐标为1,
设直线CD的解析式为y=ax+c,把C的坐标为(0,4)和点D的坐标为(4,0)代入得:$\left\{\begin{array}{l}{c=4}\\{0=4a+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{c=4}\end{array}\right.$,
∴直线CD的解析式为y=-x+4,把x=1代入得y=3,
∴E(1,3),把A(-3,0),E(1,3)代入y=kx+b得$\left\{\begin{array}{l}{-3k+b=0}\\{k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{9}{4}}\end{array}\right.$.
点评 本题主要考查了平行线平分线段定理,待定系数法求一次函数的解析式,能根据平行线分线段成比例定理求出E点坐标是解题的关键.

练习册系列答案
相关题目
 如图,△OAD≌△OBC,且∠O=65°,∠C=20°,则∠DAC=85°.
如图,△OAD≌△OBC,且∠O=65°,∠C=20°,则∠DAC=85°.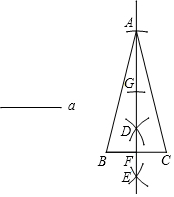 下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.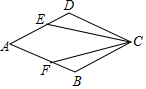 如图,菱形ABCD中,E,F分别在边AD、AB上,DE=BF.求证:EC=FC.
如图,菱形ABCD中,E,F分别在边AD、AB上,DE=BF.求证:EC=FC. 如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.
如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为23,AB:AD=1:2,△COD的周长为15,求BC的长.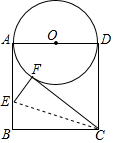 如图,正方形ABCD的边长AD为⊙O的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则tan∠AEF=$\frac{3}{4}$.
如图,正方形ABCD的边长AD为⊙O的直径,E是AB上一点,将正方形的一个角沿EC折叠,使得点B恰好与圆上的点F重合,则tan∠AEF=$\frac{3}{4}$.