题目内容
19.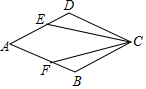 如图,菱形ABCD中,E,F分别在边AD、AB上,DE=BF.求证:EC=FC.
如图,菱形ABCD中,E,F分别在边AD、AB上,DE=BF.求证:EC=FC.
分析 先利用菱形的性质得到∠D=∠B,CD=CB,然后利用“SAS”可证明△CDE≌△CBF,从而得到EC=FC.
解答 证明:∵四边形ABCD为菱形,
∴∠D=∠B,CD=CB,
在△CDE和△CBF中
$\left\{\begin{array}{l}{DE=BF}\\{∠D=∠B}\\{CD=CB}\end{array}\right.$,
∴△CDE≌△CBF,
∴EC=FC.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.菱形的面积等于对角线乘积的一半.

练习册系列答案
相关题目
9.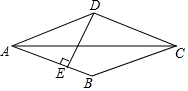 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )| A. | $\frac{75}{13}$ | B. | $\frac{96}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{144}{13}$ |
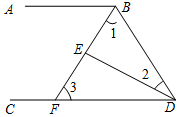 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.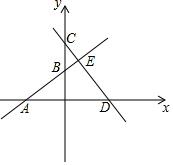 如图,一次函数y=kx+b的图象交x轴于点A(-3,0),交y轴于点B,交直线CD于E,且点C的坐标为(0,4),点D的坐标为(4,0),AB:BE=3:1,求k、b的值.
如图,一次函数y=kx+b的图象交x轴于点A(-3,0),交y轴于点B,交直线CD于E,且点C的坐标为(0,4),点D的坐标为(4,0),AB:BE=3:1,求k、b的值.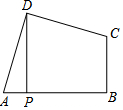 如图,在面积为16的四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,则DP的长是4.
如图,在面积为16的四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,则DP的长是4.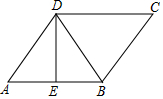 如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.
如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.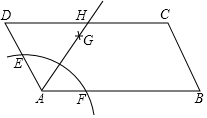 如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )
如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )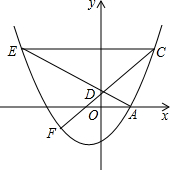 如图,抛物线y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.
如图,抛物线y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.