题目内容
9.有一段河道需要进行清淤疏通,现有甲乙两家清淤公司可供选择,如果甲公司单独做4天,乙公司再单独做6天,那么恰好能完成全部清淤任务的一半;如果甲公司先做4天,剩下的清淤工作由乙公司单独完成,那么乙公司所用时间恰好比甲公司单独完成清淤任务所需时间多2天,求甲乙两公司单独完成清淤任务各需多少天.分析 设甲公司单独完成清淤任务需要x天,乙公司单独完成清淤任务需要y天,根据总工程量=甲完成的部分+乙完成的部分,即可得出关于x、y的方程组,解之经检验后即可得出结论.
解答 解:设甲公司单独完成清淤任务需要x天,乙公司单独完成清淤任务需要y天,
根据题意得:$\left\{\begin{array}{l}{\frac{4}{x}+\frac{6}{y}=\frac{1}{2}}\\{\frac{4}{x}+\frac{x+2}{y}=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=-4}\end{array}\right.$(舍去),$\left\{\begin{array}{l}{{x}_{2}=16}\\{{y}_{2}=24}\end{array}\right.$,
经检验,x=16、y=24为原方程的解.
答:甲公司单独完成清淤任务需要16天,乙公司单独完成清淤任务需要24天.
点评 本题考查了分式方程的应用以及解方程组,找准等量关系,找出分式方程组是解题的关键.

练习册系列答案
相关题目
4.一次函数y=-2x+3的图象与y轴的交点坐标是( )
| A. | (3,1) | B. | ($\frac{3}{2}$,1) | C. | (3,0) | D. | (0,3) |
14.在“我为贫困留守儿童献爱心”捐款活动中,某校八年级(2)班50名同学捐款情况如下表:
在这次活动中,该班同学捐款金额的众数是( )
| 金额/元 | 20 | 30 | 35 | 50 | 100 |
| 学生/人 | 8 | 10 | 6 | 18 | 8 |
| A. | 50元 | B. | 100元 | C. | 35元 | D. | 30元 |
1.一个多项式分解因式的结果是x(x-2)2,则该多项式为( )
| A. | x2-2x | B. | x3-2x2 | C. | x2-4x+4 | D. | x3-4x2+4x |
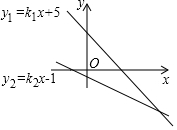 有两个一次函数:y1=k1x+5,y2=k2x-1.它们的图象交于点(5,-3),如图.那么,不等式(k1-k2)x<-6的解集是x>5.
有两个一次函数:y1=k1x+5,y2=k2x-1.它们的图象交于点(5,-3),如图.那么,不等式(k1-k2)x<-6的解集是x>5.