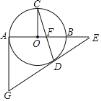
题目内容
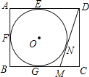
【题目】如图,![]() 为
为![]() 直径,
直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,弦
,弦![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,使
,使![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求弧
,求弧![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)6.
;(3)6.
【解析】
(1)连接OD,如图,先证明∠3=∠1,再证明∠C=∠4,然后利用∠3+∠C=90°得到∠1+∠4=90°,则OD⊥DE,然后根据切线的判定定理即可得到结论;
(2)由切线的性质得∠OAG=90°,则利用四边形内角和可计算出∠AOD=130°,然后根据弧长公式可计算出弧![]() 的长;
的长;
(3)设OF=x,则OB=3x,则可表示出BF=2x,再利用∠1=∠2得到ED=EF=2x+4,然后在Rt△ODE中,根据勾股定理得到(3x)2+(2x+4)2=(4+3x)2,再解方程求出x即可得到OB的长.
(1)连接OD.如图,∵∠1=∠2,而∠2=∠3,∴∠3=∠1.
∵OC⊥AB,∴∠3+∠C=90°,∴∠1+∠C=90°.
∵OC=OD,∴∠C=∠4,∴∠1+∠4=90°,即∠ODE=90°,∴OD⊥DE,∴GE是⊙O的切线;
(2)∵AG为切线,∴AG⊥AB,∴∠OAG=90°,而∠ODG=90°,∴∠AOD=180°﹣50°=130°,∴弧![]() 的长=
的长=![]() =
=![]() π;
π;
(3)设OF=x,则OB=3x,∴BF=2x.
∵∠1=∠2,∴ED=EF=2x+4.
在Rt△ODE中,∵OD2+DE2=OE2,∴(3x)2+(2x+4)2=(4+3x)2,解得:x=2,∴OB=3x=6.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?