题目内容
18.关于x的方程x2+2(k+1)x+k2+$\frac{1}{4}$=0的两实根之和为m,且满足m=-2(k+1),关于y的不等式组$\left\{\begin{array}{l}{y>-4}\\{y<m}\end{array}\right.$的整数解有2个,则k的取值范围是-$\frac{3}{8}$≤k<0.分析 先利用判别式的意义得到k≥-$\frac{3}{8}$,再根据根与系数的关系得m=-2(k+1),由于不等式组$\left\{\begin{array}{l}{y>-4}\\{y<m}\end{array}\right.$的整数解有2个,即整数解为-3,-2,所以-2<m≤-1,于是得到-2<-2(k+1)≤-1,解得-$\frac{1}{2}$≤k<0,然后写出k的取值范围.
解答 解:根据题意得△=4(k+1)2-4(k2+$\frac{1}{4}$)≥0,解得k≥-$\frac{3}{8}$,
m=-2(k+1),
∵不等式组$\left\{\begin{array}{l}{y>-4}\\{y<m}\end{array}\right.$的整数解有2个,
∴-2<m≤-1,
∴-2<-2(k+1)≤-1,
∴-$\frac{1}{2}$≤k<0,
∴k的取值范围为-$\frac{3}{8}$≤k<0.
故答案为-$\frac{3}{8}$≤k<0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
8.下列图形中是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列计算正确的是( )
| A. | -5-5=0 | B. | -1+1=0 | C. | -3÷$\frac{1}{3}$=-1 | D. | 43=12 |
7.一元二次方程2x(3x-2)=(x-1)(3x-2)的解是( )
| A. | x=-1 | B. | x=$\frac{2}{3}$ | C. | x1=$\frac{2}{3}$,x2=0 | D. | x1=$\frac{2}{3}$,x2=-1 |
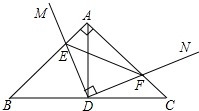 如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10.
如图,直角△ABC中,∠B=45°,AB=AC=10,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.则BE+CF=10.