题目内容
说出下列函数的开口方向、对称轴和顶点坐标:
| 函数 | 开口方向 | 对称轴 | 顶点坐标 |
| y=3x2 | |||
| y=3(x-1)2+2 | |||
| y=-4x2 | |||
| y=-4(x+2)2-4 |
考点:二次函数的性质
专题:
分析:已知抛物线解析式为顶点式,可根据顶点式求抛物线的开口方向,对称轴及顶点坐标.
解答:解:填表如下:
| 函数 | 开口方向 | 对称轴 | 顶点坐标 |
| y=3x2 | 向上 | y轴 | (0,0) |
| y=3(x-1)2+2 | 向上 | x=1 | (1,2) |
| y=-4x2 | 向下 | y轴 | (0,0) |
| y=-4(x+2)2-4 | 向下 | x=-2 | (-2,-4) |
点评:本题考查了二次函数解析式的顶点式与其性质的联系,根据二次项系数的符号确定开口方向,根据顶点式确定顶点坐标及对称轴.

练习册系列答案
相关题目
 如图,∠CAB=∠DBA,再添加一个条件,使△ABC≌△BAD,这个条件可以是
如图,∠CAB=∠DBA,再添加一个条件,使△ABC≌△BAD,这个条件可以是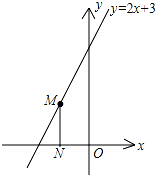 如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标
如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形,请写出符合条件的点P的坐标 如图,沿AC方向开山修路,为了加快施工速度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=150°,BD=600米,∠D=60°,当开挖点E离D
如图,沿AC方向开山修路,为了加快施工速度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=150°,BD=600米,∠D=60°,当开挖点E离D