题目内容
已知a，b满足等式M=a2+b2+20，N=4（2b-a），试判断M、N的大小关系．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：先由M-N=a2+b2+20-4（2b-a），可以得到M-N=（a+2）2+（b-4）2．由非负数的关系可以得出M与N的大小关系．
解答：解：∵M=a2+b2+20，N=4（2b-a），
∴M-N=M=a2+b2+20-4（2b-a），
∴M-N=（a+2）2+（b-4）2．
∵（a+2）2≥0，（b-4）2≥0，
∴M-N≥0，
∴M≥N．
∴M-N=M=a2+b2+20-4（2b-a），
∴M-N=（a+2）2+（b-4）2．
∵（a+2）2≥0，（b-4）2≥0，
∴M-N≥0，
∴M≥N．
点评：本题考查了配方法的运用，非负数的性质的运用，涉及了数的大小的比较．
练习册系列答案
相关题目
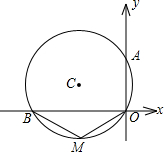如图，圆心C经过坐标原点，与两坐标轴分别交于点B，A，点A的坐标为（0，4），M为劣弧
如图，点P是半径为5的⊙O内一点，且OP=3，在过点P的所有弦中，长度为8的弦有（ ）| A、0条 | B、1条 | C、2条 | D、3条 |