题目内容
 如图,正方形ABCD的边长为4,点M在边DC上,N是M关于对角线AC的对称点,若DM=1,则说sin∠ADN=
如图,正方形ABCD的边长为4,点M在边DC上,N是M关于对角线AC的对称点,若DM=1,则说sin∠ADN=考点:轴对称的性质,锐角三角函数的定义
专题:
分析:M、N两点关于对角线AC对称,所以DM=BN,进而求出CN的长度.再由勾股定理求得DN,sin∠ADN=cos∠CDN=
=
.
| CD |
| DN |
| 4 |
| 5 |
解答: 解:在正方形ABCD中,AB=CD.
解:在正方形ABCD中,AB=CD.
∵M、N两点关于对角线AC对称,
∴BN=DM=1.
又∵sin∠ADN=sin(90°-∠CDN)=cos∠CDN,
∵CN=BC-BN=4-1=3,CD=4,
∴DN=
=5
∴sin∠ADN=cos∠CDN=
=
.
故答案为:
.
 解:在正方形ABCD中,AB=CD.
解:在正方形ABCD中,AB=CD.∵M、N两点关于对角线AC对称,
∴BN=DM=1.
又∵sin∠ADN=sin(90°-∠CDN)=cos∠CDN,
∵CN=BC-BN=4-1=3,CD=4,
∴DN=
| DC2+CN2 |
∴sin∠ADN=cos∠CDN=
| CD |
| DN |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题综合考查了正方形的性质,轴对称的性质以及锐角三角函数的定义.关键是得出sin∠ADN=cos∠CDN=
=
.
| CD |
| DN |
| 4 |
| 5 |

练习册系列答案
相关题目
(-2)3的相反数是( )
| A、-6 | B、8 | C、-8 | D、6 |

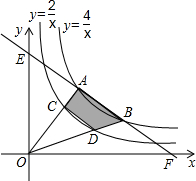 已知,如图,双曲线y=
已知,如图,双曲线y=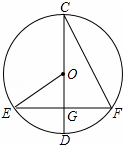 如图,⊙O的直径CD⊥EF,∠OEG=28°,则∠DCF=
如图,⊙O的直径CD⊥EF,∠OEG=28°,则∠DCF=