题目内容
已知（x2+y2）（x2+y2-1）-6=0，则x2+y2的值是（ ）
| A、3或-2 | B、-3或2 |
| C、3 | D、-2 |
考点：换元法解一元二次方程
专题：
分析：设x2+y2=t，则原方程转化为关于t的方程，通过解该方程可以求得t的值，即x2+y2的值．注意：t是非负数．
解答：解：设x2+y2=t（t≥0），则
t（t-1）-6=0，
整理得 （t-3）（t+2）=0，
解得 t1=3，t2=-2（不合题意，舍去），即x2+y2=3．
故选：C．
t（t-1）-6=0，
整理得 （t-3）（t+2）=0，
解得 t1=3，t2=-2（不合题意，舍去），即x2+y2=3．
故选：C．
点评：本题主要考查了换元法，即把某个式子看作一个整体，用一个字母去代替它，实行等量替换．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
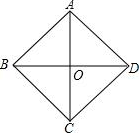如图所示，四边形ABCD中，AC、BD交于O点，AB=BC=CD=DA，求证：AC与BD互相垂直平分．
请你把五个数+（-3），（-2）2，|-2.5|，0，-（+1.5）表示在图1数轴上，并按从小到大顺序，从左到右串个糖葫芦，把数填在图2“○”内．
如图，有一只蚂蚁从一个圆柱体的下面A点爬到对应上面B点，已知圆柱的底面半径为15cm，高为12cm．试讨论蚂蚁所走过的最短路径．
如图，试写出．