题目内容
13.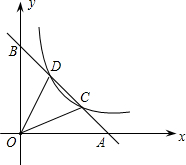 如图,直线l过点A(a,0)和点B(0,b)(其中a>0,b>0).反比例函数y=$\frac{k}{x}$(k>0)的图象与直线l交于C、D两点,连接OC、OD.
如图,直线l过点A(a,0)和点B(0,b)(其中a>0,b>0).反比例函数y=$\frac{k}{x}$(k>0)的图象与直线l交于C、D两点,连接OC、OD.(1)若a+b=10,△AOB的面积为S,问:当b为何值时,S取最大值?并求出这个最大值;
(2)当S取最大值时,若C,D恰好是线段AB的三等分点,求k的值.
分析 (1)求出面积表达式,得到S=$\frac{1}{2}$b(10-b)=-$\frac{1}{2}$b2+5b=-$\frac{1}{2}$(b-5)2+$\frac{25}{2}$,从而求出S的最大值;
(2)当C,D是线段AB的三等分点时,△AOC、△COD、△BOD的面积都相等,据此求出C点的纵坐标,将y=$\frac{5}{3}$代入y=-x+5,得x=$\frac{10}{3}$,即点C的坐标为($\frac{10}{3}$,$\frac{5}{3}$),从而得到k的值.
解答 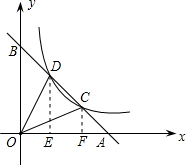 解:(1)根据题意,得:OA=a,OB=b,
解:(1)根据题意,得:OA=a,OB=b,
∴S=$\frac{1}{2}$ab,
又由a+b=10,得 a=10-b,
得:S=$\frac{1}{2}$b(10-b)=-$\frac{1}{2}$b2+5b=-$\frac{1}{2}$(b-5)2+$\frac{25}{2}$,
∵-$\frac{1}{2}$<0,
∴S有最大值,当b=5时,S取得最大值$\frac{25}{2}$.
(2)设直线l的解析式为y=mx+n,因为直线l过点A(5,0),B(0,5)
∴$\left\{\begin{array}{l}5m+n=0\\ n=5\end{array}\right.$,解得:$\left\{\begin{array}{l}m=-1\\ n=5\end{array}\right.$;
∴直线l的函数关系式为y=-x+5.
过点C作x轴的垂线,垂足为F,
当C,D是线段AB的三等分点时,△AOC、△COD、△BOD的面积都相等,
有S△AOC=$\frac{1}{3}$S△AOB,即$\frac{1}{2}$OA×CF=$\frac{1}{3}$×$\frac{1}{2}$OA×OB,
∴CF=$\frac{5}{3}$即C点的纵坐标为$\frac{5}{3}$;
将y=$\frac{5}{3}$代入y=-x+5,得x=$\frac{10}{3}$.
即点C的坐标为($\frac{10}{3}$,$\frac{5}{3}$),
∵点C在反比例函数y=$\frac{k}{x}$的图象上,
∴k=$\frac{10}{3}$×$\frac{5}{3}$=$\frac{50}{9}$.
点评 本题考查了反比例函数综合题,涉及三角形的面积公式、反比例函数图象上点的坐标特征、待定系数法求函数解析式、二次函数的最值等知识,比较复杂.

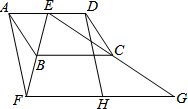 如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH. =-10,
=-10, =4,
=4, =1,求:
=1,求: 的值.
的值. 已知如图,矩形OCBD如图所示,OD=2,OC=3,反比例函数的图象经过点B,点A为第一象限双曲线上的动点(点B除外),过点A作AF⊥BD于点F,AE⊥x轴于点E,若矩形OCBD和矩形AEDF相似,则点A的坐标是($\sqrt{5}$+1,$\frac{3\sqrt{5}-3}{2}$)或($\sqrt{10}$+1,$\frac{2\sqrt{10}-2}{3}$).
已知如图,矩形OCBD如图所示,OD=2,OC=3,反比例函数的图象经过点B,点A为第一象限双曲线上的动点(点B除外),过点A作AF⊥BD于点F,AE⊥x轴于点E,若矩形OCBD和矩形AEDF相似,则点A的坐标是($\sqrt{5}$+1,$\frac{3\sqrt{5}-3}{2}$)或($\sqrt{10}$+1,$\frac{2\sqrt{10}-2}{3}$).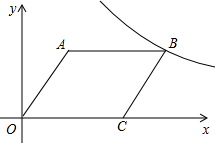 如图所示,在平面直角坐标系中,已知四边形AOBC都是菱形,且A(3,4),若在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,写出点B和点C的坐标,求反比例函数解析式.
如图所示,在平面直角坐标系中,已知四边形AOBC都是菱形,且A(3,4),若在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,写出点B和点C的坐标,求反比例函数解析式.
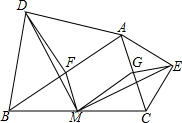 如图,在△ABC中,分别以AB、AC为斜边,向△ABC外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点,求证:△DFM≌△MGE.
如图,在△ABC中,分别以AB、AC为斜边,向△ABC外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点,求证:△DFM≌△MGE.