题目内容
7.在Rt△ABC中,∠C=90°,c为斜边,a、b为直角边,则化简$\sqrt{{{(a-b+c)}^2}}$-|c-a-b|的结果2c-2b.分析 根据三角形三边关系得到a-b+c>0,c-a-b<0,根据二次根式的性质化简即可.
解答 解:∵a+c>b,
∴a-b+c>0,
∵a+b>c,
∴c-a-b<0,
∴$\sqrt{{{(a-b+c)}^2}}$-|c-a-b|=a-b+c-a-b+c=2c-2b,
故答案为:2c-2b.
点评 本题考查的是二次根式的性质,性质:$\sqrt{{a}^{2}}$=|a|.

练习册系列答案
相关题目
18.下列各数:-2.5,0,8,-2,$\frac{π}{2}$,$\frac{5}{3}$,-0.5252252225…(每两个5之间依次增加1个2)中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下列运算正确的是( )
| A. | (2x2)3=6x6 | B. | x6÷x3=x2 | C. | 3x2-x2=3 | D. | x•x4=x5 |
16.定义两种新运算“△”和“*”,a△b=a2-ab,a*b=3a-b2,则($\sqrt{2}$△1)△($\frac{\sqrt{2}}{3}$*$\sqrt{2}$)的值为( )
| A. | 8+12$\sqrt{2}$ | B. | 8-12$\sqrt{2}$ | C. | 12+8$\sqrt{2}$ | D. | 12-8$\sqrt{2}$ |
17.如果关于x的方程(m+2)x2-2(m+1)x+m=0有且只有一个实数根,那么关于x的方程(m+1)x2-2mx+m-1=0的根为( )
| A. | -1或-3 | B. | 1或3 | C. | -1或3 | D. | 1或-3 |
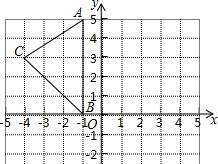 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),在图中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1点关于x轴对称的点的坐标.
如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),在图中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1点关于x轴对称的点的坐标.