题目内容
12.已知抛物线y=-x2+mx+4的顶点为D,它与x轴交于A和B两点,且A在原点左侧,B在原点右侧,与y轴的交点为P,且以AD为直径的圆M截y轴所得的弦EF恰好以点P为中点,则m的值为4或-4.分析 先求得P的坐标,根据题意得出M的纵坐标为4,进而得出D的纵坐标为8,然后根据顶点公式列出等式,解根据m的方程即可.
解答 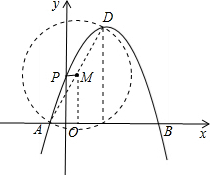 解:如图,由抛物线y=-x2+mx+4可知与y轴的交点P(0,4),
解:如图,由抛物线y=-x2+mx+4可知与y轴的交点P(0,4),
∵以AD为直径的圆M截y轴所得的弦EF恰好以点P为中点,
∴MP⊥y轴,
∴M的纵坐标为4,
∴D的纵坐标为8,
由抛物线y=-x2+mx+4的顶点的纵坐标为:$\frac{4ac-{b}^{2}}{4a}$=$\frac{-16-{m}^{2}}{-4}$=8,
整理得,m2=16,
解得m=±4,
故答案为4或-4.
点评 本题考查了抛物线和x轴的交点,垂径定理的应用以及三角形中位线的性质,求得M的纵坐标是解题的关键.

练习册系列答案
相关题目
2.如果-2x2yb和6xay5是同类项,那么a+b=( )
| A. | 7 | B. | 5 | C. | -5 | D. | -7 |
20.已知△ABC中,AB=3,BC=4,那么边AC的长可能是( )
| A. | 8 | B. | 7 | C. | 2 | D. | 1 |