题目内容
函数
（k≠0）的图象如图所示，那么函数y=kx-k的图象大致是（ ）A．
B．
C．
D．
【答案】分析：首先由反比例函数y=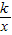
的图象位于第二、四象限，得出k＜0，则-k＞0，所以一次函数图象经过第二四象限且与y轴正半轴相交．
解答：解：∵反比例函数y=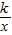
的图象位于第二、四象限，
∴k＜0，-k＞0．
∵k＜0，∴函数y=kx-k的图象过二、四象限．
又∵-k＞0，
∴函数y=kx-k的图象与y轴相交于正半轴，
∴一次函数y=kx-k的图象过一、二、四象限．
故选C．
点评：本题考查的知识点：
（1）反比例函数y=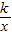
的图象是双曲线，当k＜0时，它的两个分支分别位于第二、四象限．
（2）一次函数y=kx+b的图象当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限．
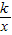的图象位于第二、四象限，得出k＜0，则-k＞0，所以一次函数图象经过第二四象限且与y轴正半轴相交．解答：解：∵反比例函数y=
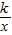的图象位于第二、四象限，∴k＜0，-k＞0．
∵k＜0，∴函数y=kx-k的图象过二、四象限．
又∵-k＞0，
∴函数y=kx-k的图象与y轴相交于正半轴，
∴一次函数y=kx-k的图象过一、二、四象限．
故选C．
点评：本题考查的知识点：
（1）反比例函数y=
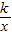的图象是双曲线，当k＜0时，它的两个分支分别位于第二、四象限．（2）一次函数y=kx+b的图象当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限．
练习册系列答案
相关题目
在，请求出所有满足条件的D点坐标；若不存在，请说明理由．
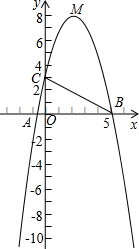如图，二次函数y=-x2+px+q的图象与x轴交于A、B两点，与y轴交于点C（0，3），顶点M在第一象限，∠ABC=30°．