Question

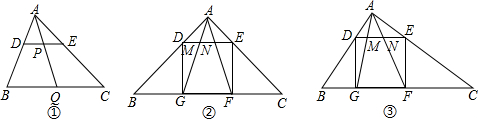
如图，已知正方形ABCD的边长为1，以顶点A、B为圆心，1为半径的两弧交于点E，以顶点C、D为圆心，1为半径的两弧交于点F，则EF的长为（　　）

• A、

  2

  3

• B、

  3

  2

• C、2-

  3

• D、

  3

  -1

Answer 1

考点：正方形的性质

专题：

分析：连接AE，BE，DF，CF，可证明三角形AEB是等边三角形，利用等边三角形的性质和勾股定理即可求出边AB上的高线，同理可求出CD边上的高线，进而求出EF的长．

解答：解：连接AE，BE，DF，CF．
∵以顶点A、B为圆心，1为半径的两弧交于点E，AB=1，
∴AB=AE=BE，
∴△AEB是等边三角形，
∴边AB上的高线为EN=

3

2

，
延长EF交AB于N，并反向延长EF交DC于M，则E、F、M，N共线，
则EM=1-EN=1-

3

2

，
∴NF=EM=1-

3

2

，
∴EF=1-EM-NF=

3

-1．
故选D．

点评：本题考查了正方形的性质和等边三角形的判定和性质以及勾股定理的运用，解题的关键是添加辅助线构造等边三角形，利用等边三角形的性质解答即可．