Question

【题目】如图，点在反比例函数第一象限的图象上，连接，延长与双曲线的另一支交于点，作的垂直平分线，交于点，交轴于点，交轴于点．

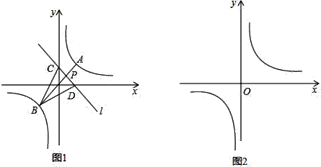
(1)在图中，当，直接写出，，三点的坐标，并求出直线的解析式．

(2)当点的坐标为时，利用图，求的面积．

Answer 1

【答案】（1）B点的坐标是,P点的坐标是 ，A点的坐标是，直线l的解析式为：；（2）.

【解析】

（1）过P作PM⊥OD于点M，根据BD=BC，BA⊥CD，PO=PA得出四边形ODAC是正方形，再求出S正方形ODAC=12，得出OD=AD=，从而求出A、B点的坐标，再根据，求出P点的坐标即可,设一次函数一般式为：y=kx+b，将点P和点D坐标分别代入，列出方程组，求解即可求出k和b的值，从而求出解析式；

（2）过A作AN⊥OD于点N，先求出OP的长，根据△OPM∽△ODP得出求出DP，根据P点是OA的中点，求出AB=10，最后根据代入计算即可．

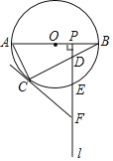
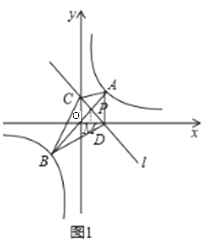
(1)如图1:过P作PM⊥OD于点M,

∵BD=BC，BA⊥CD，

∴PC=PD，

∵PO=PA，

∴四边形ODAC是菱形，

∵∠COD=90°，

∴四边形ODAC是正方形，

∵点A在反比例函数第一象限的图象上，

∴S正方形ODAC=12，

,

∴A点的坐标是，，

∴B点的坐标是,P点的坐标是，D点坐标是，

设直线l的解析式为：y=kx+b，

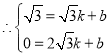,解得：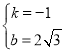

∴直线l的解析式为：；

(2) 如图2:过A作AN⊥OD于点N，

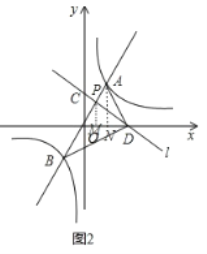
∵点P的坐标为,

,

,

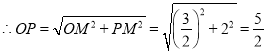∵DP⊥OP，PM⊥OM，

∴△OPM∽△ODP，

∴，

∴，

∴，

∵P点是OA的中点，

∴AO=2OP=5，

∴BO=5，

∴AB=10，

∴.