题目内容

6．如果$\sqrt{{a}^{2}-16a+64}$=8-a成立，那么实数a的取值范围是（　　）
A．a≤0B．a≤8C．a≥-8D．a≥8

分析 直接利用二次根式的性质得出8-a≥0进而得出答案．

解答 解：∵$\sqrt{{a}^{2}-16a+64}$=$\sqrt{（a-8）^{2}}$=8-a，
∴8-a≥0，
解得：a≤8．
故选：B．

点评 此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．

练习册系列答案
相关题目
16．下列说法正确的是（　　）
A．掷一枚均匀的骰子，骰子停止运动后，6点朝上是必然事件
B．太阳从西边升起是不可能事件
C．“明天降雨的概率为$\frac{1}{2}$”，表示明天有半天都在降雨
D．一个游戏中奖的概率是$\frac{1}{100}$，则做100次这样的游戏一定会中奖
17．小芳是一位爱动脑的同学，她先剪下一段铁丝的“一半少1cm”，又剪下剩下铁丝的“$\frac{3}{4}$多2cm”．她惊喜地发现：剪下的两段铁丝同样长！求这段铁丝的长度．
14．已知（a2-1）x2-（a+1）x+8=0是关于x的一元一次方程．求代数式199（a+x）（x-2a）+3a+4的值．
1．已知：2+$\frac{2}{3}$=22×$\frac{2}{3}$，3+$\frac{3}{8}$=32×$\frac{3}{8}$，4+$\frac{4}{15}$=42×$\frac{4}{15}$，…若10+$\frac{a}{b}$=102×$\frac{a}{b}$（a、b为正整数），求分式$\frac{{a}^{2}+2ab+{b}^{2}}{a{b}^{2}+{a}^{2}b}$•$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$的值．
11．仔细阅读下列材料．
“分数均可化为有限小数或无限循环小数”．反之，“有限小数或无限循环小数均可化为分数”
例如：$\frac{1}{4}$=1÷4=0.25，1$\frac{3}{5}$=1+$\frac{3}{5}$=1+0.6=1.6或1$\frac{3}{5}$=$\frac{8}{5}$=8÷5=1.6，$\frac{1}{3}$=1÷3=0.$\stackrel{•}{3}$，
反之，0.25=$\frac{25}{100}$=$\frac{1}{4}$，1.6=1+0.6=1+$\frac{6}{10}$=1$\frac{3}{5}$或1.6=$\frac{16}{10}$=$\frac{8}{5}$，
那么0.$\stackrel{•}{3}$怎么化为$\frac{1}{3}$呢？
解：∵0.$\stackrel{•}{3}$×10=3.$\stackrel{•}{3}$=3+0.$\stackrel{•}{3}$
∴不妨设0.$\stackrel{•}{3}$=x，则上式变为10x=3+x，解得x=$\frac{1}{3}$ 即0.$\stackrel{•}{3}$=$\frac{1}{3}$
根据以上材料，回答下列问题．
（1）将“分数化为小数”：$\frac{7}{4}$=1.75；$\frac{4}{11}$=0.$\stackrel{•}{3}\stackrel{•}{6}$．
（2）将“小数化为分数”：0.$\stackrel{•}{4}$=$\frac{4}{9}$；1.5$\stackrel{•}{3}$=$\frac{23}{15}$．
（3）将小数1.$\stackrel{•}{0}$$\stackrel{•}{2}$化为分数，需写出推理过程．
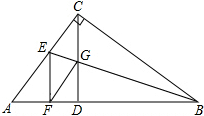18．如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，BE平分∠ABC交CD、AC分别于G、E，GF∥AC交AB于F．
（1）求证：△FBG≌△CBG；
（2）猜想：EF与AB有怎样的位置关系，请说明理由．
15．计算（$\frac{{a}^{2}-{b}^{2}}{ab}$）3（$\frac{a}{b-a}$）3，结果等于-$\frac{（a+b）^{3}}{{b}^{3}}$．
16．到平面内不在同一条直线上三点距离相等的点有1个，它是线段垂直平分线的交点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网