题目内容
已知抛物线y=3x2+m-1与x轴两交点为A、B,且AB=3,求抛物线的解析式及顶点坐标.
考点:抛物线与x轴的交点
专题:
分析:令y=0,则3x2+m-1=0,利用根与系数的关系和AB=3来求m的值;然后将抛物线解析式转化顶点式,根据解析式写出顶点坐标.
解答:解:y=0,则3x2+m-1=0.
设点A、B的横坐标分别是a、b(a>b).则
a+b=0,ab=
,且
∵AB=3,
∴a-b=
=
=3,
整理,得m=-
.
故抛物线的解析式为:y=3x2-
.
其顶点坐标是(0,-
).
设点A、B的横坐标分别是a、b(a>b).则
a+b=0,ab=
| m-1 |
| 3 |
∵AB=3,
∴a-b=
| (a+b)2-4ab |
-
|
整理,得m=-
| 23 |
| 4 |
故抛物线的解析式为:y=3x2-
| 27 |
| 4 |
其顶点坐标是(0,-
| 27 |
| 4 |
点评:本题考查了抛物线与x轴的交点.此题也可以根据该抛物线的对称轴是y轴求得点A或B的坐标,利用代入法求得m的值.

练习册系列答案
相关题目
不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
 A、B、C各点的位置如图.
A、B、C各点的位置如图.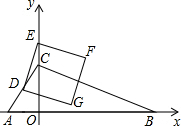 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=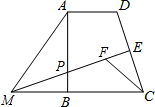 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E是CD的中点,过点E作CD的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E是CD的中点,过点E作CD的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA. 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为