题目内容
5. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B.求证:ED=EF.
如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B.求证:ED=EF.
分析 首先求出∠BDE=∠CEF,再利用ASA证明△BDE≌△CEF,即可得出结论.
解答 证明:∵∠CED是△BDE的外角,
∴∠CED=∠B+∠BDE,
∵∠DEF=∠B,
∴∠BDE=∠CEF;
在△BDE与△CEF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{BD=CE}\\{∠BDE=∠CEF}\end{array}\right.$,
∴△BDE≌△CEF(ASA),
∴DE=EF.
点评 该题主要考查了三角形的外角的性质、全等三角形的判定及其性质等几何知识点及其应用问题;牢固掌握三角形外角的知识、全等三角形的判定及其性质等几何知识点是基础,灵活运用、解题是关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
15.在平面直角坐标系中,平移二次函数y=(x-2015)(x-2017)+3的图象,使其与x轴两交点间的距离为2个单位长度,则下列平移方式中可实现上述要求的是( )
| A. | 向上平移3个单位 | B. | 向下平移3个单位 | C. | 向左平移3个单位 | D. | 向右平移3个单位 |
14.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出两个小球,两球恰好是一个黄球和一个红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
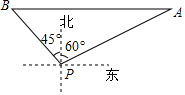 如图,一艘轮船位于灯塔P北偏东60°方向上,距离灯塔40海里的A处,它向西航行多少海里到达灯塔P北偏西45°方向上的B处.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)
如图,一艘轮船位于灯塔P北偏东60°方向上,距离灯塔40海里的A处,它向西航行多少海里到达灯塔P北偏西45°方向上的B处.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1) 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线上y=-$\frac{3}{4}$x上,求点B与其对应点B′间的距离.
如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线上y=-$\frac{3}{4}$x上,求点B与其对应点B′间的距离.