题目内容
4. 如图,∠B=∠ACD=90°,AB=4,AC=5,当AD=$\frac{25}{3}$或$\frac{25}{4}$时,这两个直角三角形相似.
如图,∠B=∠ACD=90°,AB=4,AC=5,当AD=$\frac{25}{3}$或$\frac{25}{4}$时,这两个直角三角形相似.
分析 先利用勾股定理计算出BC=3,再分类讨论:由于∠B=∠ACD=90°,则根据两组对应边的比相等且夹角对应相等的两个三角形相似,当AB:CD=BC:AC时,△ABC∽△DCA;当AB:AC=BC:CD时,△ABC∽△ACD,然后分别利用比例性质求出CD,再利用勾股定理计算对应的AD的长.
解答 解:在Rt△ABC中,BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵∠B=∠ACD=90°,
∴当AB:CD=BC:AC时,△ABC∽△DCA,即4:CD=3:5,解得CD=$\frac{20}{3}$,此时AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\frac{25}{3}$;
当AB:AC=BC:CD时,△ABC∽△ACD,即4:5=3:CD,解得CD=$\frac{15}{4}$,此时AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\frac{25}{4}$;
综上所述,当AD=$\frac{25}{3}$或$\frac{25}{4}$时,这两个直角三角形相似.
故答案为$\frac{25}{3}$或$\frac{25}{4}$.
点评 本题考查了相似三角形判定:两组对应边的比相等且夹角对应相等的两个三角形相似;注意利用对应边的变换进行分类讨论.

练习册系列答案
相关题目
12. 如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
 如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )| A. | 63°30′ | B. | 53°30′ | C. | 73°30′ | D. | 93°30′ |
9. 实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )
实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )
 实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )
实数a,b在数轴上的位置如图所示,化简|a+b|+|a-b|+|b-a|的结果为( )| A. | A.-3a+b | B. | a+b | C. | -a+3b | D. | -a-b |
16.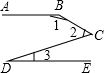 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )
 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=180° | C. | ∠1=∠2+∠3 | D. | ∠1-∠2+∠3=180° |
13.若2m2-3m-7=0,7n2+3n-2=0,其中m,n为实数,且mn≠1,则m+$\frac{1}{n}$=( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{2}$ | D. | $-\frac{7}{2}$ |
 与
与 的大小有什么关系?为什么?
的大小有什么关系?为什么?
 如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG.
如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG. 如图所示,三角形ABC是直角三角形,∠ABC=60°,若在直线AC或BC上取一点P,使得三角形PAB为等腰三角形,那么这样的点P的个数为( )
如图所示,三角形ABC是直角三角形,∠ABC=60°,若在直线AC或BC上取一点P,使得三角形PAB为等腰三角形,那么这样的点P的个数为( )