题目内容
19.在?ABCD中,AB=AC,CE是AB边上的高,若AB=AC=5,CE=4,则AD=2$\sqrt{5}$或4$\sqrt{5}$.分析 分∠BAC为锐角和钝角两种情况考虑,在Rt△AEC中通过勾股定理求出线段AE的长度,再根据边与边的关系找出线段BE的长度,最后在Rt△BEC中通过勾股定理求出线段AD的长度即可.
解答 解:①当∠BAC为锐角时,如图1所示.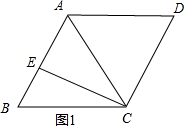
在Rt△AEC中,AC=5,CE=4,∠AEC=90°,
∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∵AB=5,AB=AE+BE,
∴BE=2.
在Rt△BEC中,CE=4,BE=2,∠BEC=90°,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$;
②当∠BAC为钝角时,如图2所示.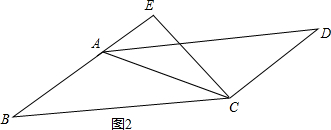
在Rt△AEC中,AC=5,CE=4,∠AEC=90°,
∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∵AB=5,AB=BE-AE,
∴BE=8.
在Rt△BEC中,CE=4,BE=8,∠BEC=90°,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$.
综上可知:AD的长度为2$\sqrt{5}$或4$\sqrt{5}$.
故答案为:2$\sqrt{5}$或4$\sqrt{5}$.
点评 本题考查了平行四边形的性质以及勾股定理,解题的关键是求出线段BE的长度.本题属于基础题,难度不大,解决该题型题目时,分类讨论是关键,解决该题型时,部分同学往往只考虑到了第一种情况,在以后的练习中要注意考虑问题全面性的培养.

练习册系列答案
相关题目
7.下列命题中真命题的个数是( )
①两条对角线相等的四边形是矩形 ②菱形是中心对称图形,不是轴对称图形
③对角线互相垂直且相等的四边形是正方形 ④依次连结矩形各边的中点,所得四边形是菱形.
①两条对角线相等的四边形是矩形 ②菱形是中心对称图形,不是轴对称图形
③对角线互相垂直且相等的四边形是正方形 ④依次连结矩形各边的中点,所得四边形是菱形.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.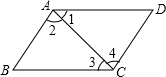 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
 如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )| A. | ∠1=∠3 | B. | ∠B+∠BCD=180° | C. | ∠2=∠4 | D. | ∠D+∠BAD=180° |
4.下列各式属于最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{6}$ | D. | $\sqrt{8}$ |
8.平行四边形、矩形、菱形、正方形都具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 对角线互相垂直平分且相等 |
9.根据下列表述,能确定具体位置的是( )
| A. | 奥斯卡影院2号厅3排 | B. | 汝南县汝宁大街 | ||
| C. | 东经118° | D. | 天中山北偏东60°,10km处 |
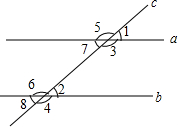 如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )