Question

【题目】已知二次函数y=ax2+bx+c图象的对称轴为y轴，且过点(1，2)，(2，5)．

（1）求二次函数的解析式；

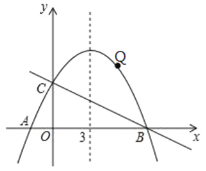
（2）如图，过点E(O，2)的一次函数图象与二次函数的图象交于A，B两点（A点在B点的左侧），过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D。

①当CD=3时，求该一次函数的解析式；

②分别用S1，S2，S3表示△ACE，△ECD，△EDB的面积，问是否存在实数t，使得=tS1S3，都成立？若存在，求出t的值；若不存在，说明理由。

Answer 1

【答案】（1）；（2）①或，②存在实数，使得成立，理由见解析

【解析】

（1）根据对称轴方程、和过点(1，2)，(2，5)，用待定系数法即可解答．

（2）①设过点的一次函数的解析式为，则，解得m=2,即该一次函数的解析式为. 设，，则，.将代入，得，再由即可求出解得k，所以一次函数的解析式是或.

②根据三角形面积公式可得，，，所以，即S1S3=-x1y1·x2y2=- x1 x2(kx1+2)( kx2+2)= - x1 x2[k2x1x2+2k(x1 +x2)+4]从而求解.

（1）依题意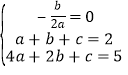，得，解得，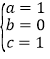

∴二次函数的解析式为.

（2）设过点的一次函数的解析式为，

则，

∴，

即该一次函数的解析式为.

设，，则，.

将代入，得，

即，

解得，

∴，.

①依题意，

得，

∵，

∴，

解得，

∴该一次函数的解析式是或.

②依题意，得，

，

，

∴，

.

∵，，

∴，，

，

∴，

故存在实数，使得成立.