Question

【题目】如图所示是二次函数y＝ax2+bx+c（a≠0）图象的一部分，直线x＝﹣1是对称轴，有下列判断：①b﹣2a＝0，②4a﹣2b+c＜0，③a﹣b+c＝﹣9a，④若（﹣3，y1），（，y2）是抛物线上的两点，则y1＜y2．其中正确的是（　　）

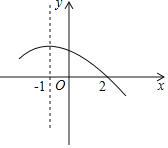
A. ①②③B. ①③C. ①④D. ①③④

Answer 1

【答案】B

【解析】

根据二次函数的开口方向，与x轴交点的个数，与y轴交点的位置、对称轴的位置即可判断．

①∵对称轴为x=-1，

∴-=-1，

∴b-2a=0，故①正确；

由于对称轴为x=-1，

∴（2，0）的对称点为（-4，0）

∴当-4＜x＜2时，y＞0，

令x=-2代入y=ax2+bx+c

∴y=4a-2b+c＞0，故②错误

令x=2代入y=ax2+bx+c，

∴4a+2b+c=0，

∵b=2a，

∴c=-4a-2b=-4a-4a=-8a，

令x=-1代入y=ax2+bx+c，

∴y=a-b+c=a-2a-8a=-9a，故③正确，

∵对称轴为x=-1，

∴（-3，y1）关于x=-1的对称点为（1，y1）

∵x＞-1时，y随着x的增大而减少，

∴当1＜时，

∴y1＞y2，故④错误，

故选B．