题目内容
10.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7跟火柴,第2个图案需13跟火柴,…,依此规律,第42个图案需1893根火柴.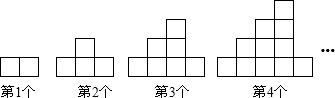
分析 由图形可知:第1个图案需7根火柴,7=1×(1+3)+3,第2个图案需13根火柴,13=2×(2+3)+3,第3个图案需21根火柴,21=3×(3+3)+3,…得出规律第n个图案需n(n+3)+3根火柴,再把42代入即可求出答案.
解答 解:根据题意可知:
第1个图案需7根火柴,7=1×(1+3)+3,
第2个图案需13根火柴,13=2×(2+3)+3,
第3个图案需21根火柴,21=3×(3+3)+3,
…,
第n个图案需n(n+3)+3根火柴,
则第42个图案需:42×(42+3)+3=1893根.
故答案为:1893.
点评 此题主要考查了图形的变化类,关键是根据题目中给出的图形,通过观察思考,归纳总结出规律,再利用规律解决问题.

练习册系列答案
相关题目
5.将点(0,1)绕原点顺时针旋转90°,所得的点为( )
| A. | (-1,0) | B. | (0,-1) | C. | (1,0) | D. | (1,1) |
19.抛物线y=x2先向右平移5个单位,再向上平移3个单位,则新的抛物线式是( )
| A. | y=(x-5)2+3 | B. | y=(x+5)2-3 | C. | y=(x-5)2-3 | D. | y=(x+5)2+3 |
 如图,AB∥CD,O为∠BAC和∠ACD的平分线的交点,OE⊥AC于点E,且OE=4,则两平行线间的距离为8.
如图,AB∥CD,O为∠BAC和∠ACD的平分线的交点,OE⊥AC于点E,且OE=4,则两平行线间的距离为8. 如图,要得到△ABC∽△ADE,只需要再添加一个条件是DE∥BC(答案不唯一).
如图,要得到△ABC∽△ADE,只需要再添加一个条件是DE∥BC(答案不唯一).