题目内容
1. 如图,AB∥CD,O为∠BAC和∠ACD的平分线的交点,OE⊥AC于点E,且OE=4,则两平行线间的距离为8.
如图,AB∥CD,O为∠BAC和∠ACD的平分线的交点,OE⊥AC于点E,且OE=4,则两平行线间的距离为8.
分析 过点O作MN,MN⊥AB于M,求出MN⊥CD,则MN的长度是AB和CD之间的距离;然后根据角平分线的性质,分别求出OM、ON的长度是多少,再把它们求和即可.
解答 解:如图,过点O作MN,MN⊥AB于M,交CD于N,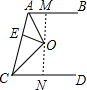
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=4,
∴OM=OE=4,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=4,
∴MN=OM+ON=8,
即AB与CD之间的距离是8.
故答案为:8.
点评 此题主要考查了角平分线的性质和平行线之间的距离的应用,要熟练掌握,解答此题的关键是要明确:①角的平分线上的点到角的两边的距离相等,②从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,③平行线间的距离处处相等.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
16.如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面圆的半径为( )
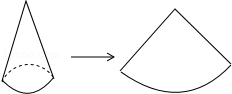

| A. | $\frac{3}{4}$π | B. | $\frac{3}{2}$π | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
6.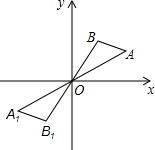 △ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(4,2),则点A1的坐标是( )
△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(4,2),则点A1的坐标是( )
 △ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(4,2),则点A1的坐标是( )
△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(4,2),则点A1的坐标是( )| A. | (4,-2) | B. | (-4,-2) | C. | (-2,-3) | D. | (-2,-4) |
13.计算:-32×(-2)3的结果是( )
| A. | 36 | B. | -36 | C. | -72 | D. | 72 |