题目内容
 如图,把两个火柴盒放倒,在这个过程中能验证勾股定理.请你试一试.
如图,把两个火柴盒放倒,在这个过程中能验证勾股定理.请你试一试.考点:勾股定理的证明
专题:
分析:四边形ACED的面积从大的一方面来说属于直角梯形,可利用直角梯形的面积公式进行表示;从组成来看,由三个直角三角形组成.应利用三角形的面积公式来进行表示.
解答: 解:连接AD,
解:连接AD,
依题意,图中的四边形ACED为直角梯形,△BDA为等腰直角三角形,
Rt△ABC和Rt△BDE的形状和大小完全一样,
设梯形ACED的面积为S,则S=
(a+b)(a+b)=
(a2+b2)+ab,
又∵S=SRt△BDA+2SRt△ABC=
c2+2×
ab=
c2+ab,
∴
(a2+b2)+ab=
c2+ab,
因此a2+b2=c2.
 解:连接AD,
解:连接AD,依题意,图中的四边形ACED为直角梯形,△BDA为等腰直角三角形,
Rt△ABC和Rt△BDE的形状和大小完全一样,
设梯形ACED的面积为S,则S=
| 1 |
| 2 |
| 1 |
| 2 |
又∵S=SRt△BDA+2SRt△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
因此a2+b2=c2.
点评:本题考查了勾股定理的证明,需注意:组成的图形的面积有两种表示方法:大的面积的表示方法和各个组成部分的面积的和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,∠ADC等于多少度?简要说明理由.
如图△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,∠ADC等于多少度?简要说明理由.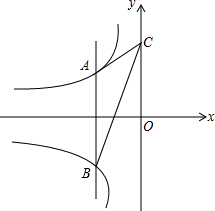 如图,动点A在双曲线y=-
如图,动点A在双曲线y=-