题目内容
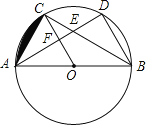
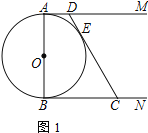
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() 为圆弧上一点,
为圆弧上一点,![]() 垂直于过
垂直于过![]() 点的切线,垂足为
点的切线,垂足为![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .
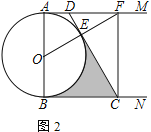
.![]() ,垂足为点
,垂足为点![]() .
.
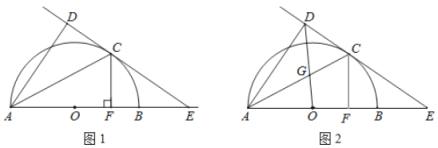
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() 时,求
时,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
1)连结OC,如图1,先利用切线的性质得到OC⊥CD,再判断OC∥AD得到∠1=∠3,加上∠2=∠3,则有∠1=∠2,于是可判断![]() ,即可得到
,即可得到![]() ;
;
(2)连结OC,如图2,先证明△OCG∽△DAG得到![]() ,即可求出
,即可求出![]() =10,Rt△OCF中利用勾股定理即可求出
=10,Rt△OCF中利用勾股定理即可求出![]() .
.
(1)连结![]() ,
,
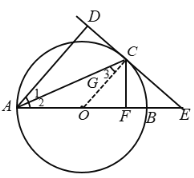
∵直线![]() 与
与![]() 相切于点
相切于点![]() ,∴
,∴![]() ,
,
∵![]() ∴
∴![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ∴
∴![]()
∴在![]() 和
和![]() 中
中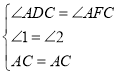
∴![]()
∴![]()
(2)连结![]() ,
,
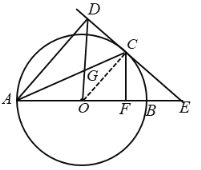
∵![]() ,∴
,∴![]() ,
,![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ∴
∴![]()
∴![]() ∴
∴![]()
由勾股定理![]()
本题考查了圆的有关概念及性质,切线的性质,相似三角形的判定与性质,勾股定理等,解题关键是熟练掌握并灵活运用相似三角形的判定与性质等.

练习册系列答案
相关题目
【题目】已知二次函数 y=ax2+bx+c,其中 y 与 x 的部分对应值如表:
x | -2 | -1 | 0.5 | 1.5 |
y | 5 | 0 | -3.75 | -3.75 |
下列结论正确的是( )
A.abc<0B.4a+2b+c>0
C.若 x<-1 或 x>3 时,y>0D.方程 ax2+bx+c=5 的解为 x1=-2,x2=3