Question

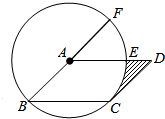如图，在?ABCD中，以点A为圆心，AB的长为半径的圆恰好与CD相切于点C，交AD于点E，延长BA与⊙A相交于点F．若

EF

的长为

π

2

，则图中阴影部分的面积为

 

．

Answer 1

考点：切线的性质,平行四边形的性质,弧长的计算,扇形面积的计算

专题：几何图形问题

分析：求图中阴影部分的面积，就要从图中分析阴影部分的面积是由哪几部分组成的．很显然图中阴影部分的面积=△ACD的面积-扇形ACE的面积，然后按各图形的面积公式计算即可．

解答：解：连接AC，
∵DC是⊙A的切线，
∴AC⊥CD，
又∵AB=AC=CD，
∴△ACD是等腰直角三角形，
∴∠CAD=45°，
又∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠CAD=∠ACB=45°，
又∵AB=AC，
∴∠ACB=∠B=45°，
∴∠FAD=∠B=45°，
∵

EF

的长为

π

2

，
∴

π

2

=

45πr

180

，
解得：r=2，
∴S_阴影=S_△ACD-S_扇形ACE=

1

2

×2×2-

45π×22

360

=2-

π

2

．
故答案为：2-

π

2

．

点评：本题主要考查了扇形的面积计算方法，不规则图形的面积通常转化为规则图形的面积的和差．