题目内容
4.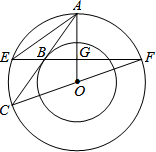 如图,以O为圆心的两个同心圆中,大圆的弦AC和小圆相切于点B,过点B作AO的垂线交大圆于E,F,垂足为G,CF恰为大圆的直径.
如图,以O为圆心的两个同心圆中,大圆的弦AC和小圆相切于点B,过点B作AO的垂线交大圆于E,F,垂足为G,CF恰为大圆的直径.(1)求证:AB=BC;
(2)求AE:AB:BE.
分析 (1)连接OB,由切线性质定理可得:OB⊥AB,再由垂径定理即可得到AB=BC;
(2)连结AF,设小圆半径为R,由△OAB∽△FBA得:$\frac{OB}{BA}=\frac{AB}{FA}$,所以AB2=OB•AF=2R2,进而可求出AB=$\sqrt{2}$R,在RT△OAB中,OA=$\sqrt{3}$R,AG=$\frac{2\sqrt{3}}{3}$R,BG=$\frac{\sqrt{6}}{3}$R,在RT△AEG中,EG=$\frac{2\sqrt{6}}{3}$R,BE=$\frac{\sqrt{6}}{3}$R,继而可得到AE:AB:BE的比值.
解答 证明:(1)连接OB,
∵AC是小圆的切线,
∴OB⊥AC,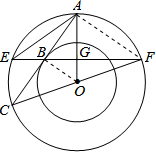
∴AB=BC;
(2)连结AF,设小圆半径为R,
∵AC是小圆的切线,
∴OB⊥AC,
∴AB=BC,
又∵FO=OC,
∴AF=2OB=2R,
∵OA⊥EF,
∴$\widehat{AE}=\widehat{AF}$,
∴AE=AF=2R,
由△OAB∽△FBA得:$\frac{OB}{BA}=\frac{AB}{FA}$,
∴AB2=OB•AF=2R2,
∴AB=$\sqrt{2}$R,
在RT△OAB中,OA=$\sqrt{3}$R,AG=$\frac{2\sqrt{3}}{3}$R,BG=$\frac{\sqrt{6}}{3}$R,
在RT△AEG中,EG=$\frac{2\sqrt{6}}{3}$R,
∴BE=$\frac{\sqrt{6}}{3}$R,
∴AE:AB:BE=$\sqrt{6}$:$\sqrt{3}$:1.
点评 本题考查了和圆有关的综合性题目,用到的知识点有切线的性质定理、垂径定理、圆周角定理、勾股定理、相似三角形的判定和性质,题目的综合性较强,难度较大,对学生的综合解题能力较高.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案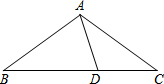 如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )
如图,在△ABC中,AB=AC,∠BAC=108°,点D在BC上,且BD=AB,连接AD,则∠CAD等于( )| A. | 30° | B. | 36° | C. | 38° | D. | 45° |
 如图,分别以点A,B为圆心作圆,使两圆都经过线段AB上一点F,这两圆的位置关系是( )
如图,分别以点A,B为圆心作圆,使两圆都经过线段AB上一点F,这两圆的位置关系是( )| A. | 相交 | B. | 内切 | C. | 外切 | D. | 外离 |
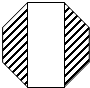 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )| A. | $10\sqrt{2}$ | B. | 20 | C. | 18 | D. | $20\sqrt{2}$ |
| A. | y=(x-1)2+2 | B. | y=(x-2)2+1 | C. | y=(x+1)2-2 | D. | y=(x+2)2-1 |