题目内容
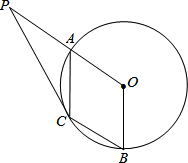 如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧
如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧 |
| AB |
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若圆O的半径R=2,求PC长.
考点:圆心角、弧、弦的关系,勾股定理,菱形的判定
专题:
分析:(1)首先连接OC,由A、B是圆O上的两点,∠AOB=120°,C是劣弧
的中点,易证得△AOC与△BOC都是等边三角形,则可得AC=OA=OC=OB=BC,继而证得四边形OACB是菱形.
(2)由AP=OA,易证得△OPC是直角三角形,然后利用勾股定理求得答案.
 |
| AB |
(2)由AP=OA,易证得△OPC是直角三角形,然后利用勾股定理求得答案.
解答: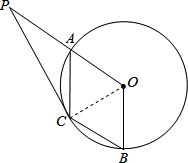 解:(1)四边形OACB是菱形.
解:(1)四边形OACB是菱形.
理由:连接OC,
∵∠AOB=120°,C是劣弧
的中点,
∴∠AOC=∠BOC=
∠AOB=60°,
∵OA=OC=OB,
∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,
∴四边形OACB是菱形.
(2)∵AP=OA,AC=OA,
∴AP=AC,
∴∠P=∠ACP=
∠OAC=30°,
∴∠OCP=90°,
∵R=2,
∴OC=2,OP=4,
∴PC=
=2
.
 解:(1)四边形OACB是菱形.
解:(1)四边形OACB是菱形.理由:连接OC,
∵∠AOB=120°,C是劣弧
 |
| AB |
∴∠AOC=∠BOC=
| 1 |
| 2 |
∵OA=OC=OB,
∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,
∴四边形OACB是菱形.
(2)∵AP=OA,AC=OA,
∴AP=AC,
∴∠P=∠ACP=
| 1 |
| 2 |
∴∠OCP=90°,
∵R=2,
∴OC=2,OP=4,
∴PC=
| OP2-OC2 |
| 3 |
点评:此题考查了弧与圆心角的关系、菱形的判定、等边三角形的判定与性质以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
将下列长度的三根木棒首尾顺次连接,不能组成直角三角形的是( )
| A、3、4、5 | ||||
| B、7、24、25 | ||||
C、1,
| ||||
| D、4、5、6 |
 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论: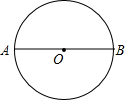 如图,已知AB为⊙O的直径,点C为半圆上的四等分点,在直径AB所在的直线上找一点P,连接CP交⊙O于点Q(异于点P),使PQ=OQ,则∠CPO=
如图,已知AB为⊙O的直径,点C为半圆上的四等分点,在直径AB所在的直线上找一点P,连接CP交⊙O于点Q(异于点P),使PQ=OQ,则∠CPO= 如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0<t≤4).解答下列问题:
如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0<t≤4).解答下列问题: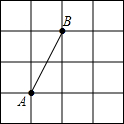 如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点.现有格点A、B,在方格中任意找一点C(必须是格点),使△ABC成为等腰三角形.这样的格点有
如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点.现有格点A、B,在方格中任意找一点C(必须是格点),使△ABC成为等腰三角形.这样的格点有