��Ŀ����
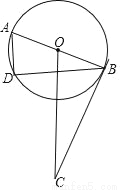
��ͼ1������ABCD�У�AB=4��AD=3���Ѿ�����ֱ��AC�۵���ʹ��B���ڵ�E����AE��CD�ڵ�F������DE��
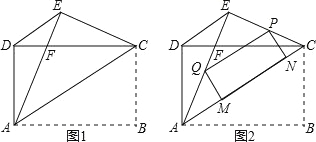
��1����֤����DEC�ա�EDA��
��2����DF��ֵ��
��3����ͼ2����PΪ�߶�EC��һ���㣬����P����AEC���ڽӾ��Σ�ʹ�䶥��Q�����߶�AE�ϣ�����M��N�����߶�AC�ϣ����߶�PE�ij�Ϊ��ֵʱ������PQMN����������������ֵ��
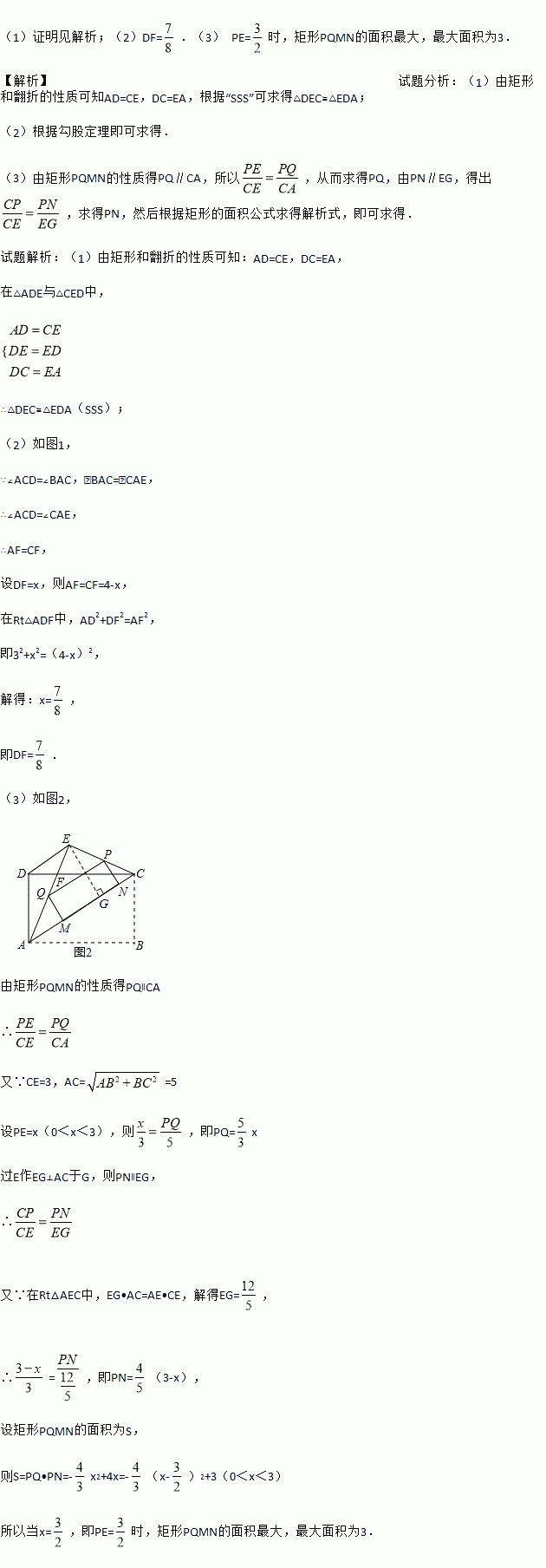
��1��֤������������2��DF=����3�� PE=ʱ������PQMN��������������Ϊ3�� �������������������1���ɾ��κͷ��۵����ʿ�֪AD=CE��DC=EA�����ݡ�SSS������á�DEC�ա�EDA�� ��2�����ݹ��ɶ���������ã� ��3���ɾ���PQMN�����ʵ�PQ��CA�����ԣ��Ӷ����PQ����PN��EG���ó������PN��Ȼ����ݾ��ε������ʽ��ý���ʽ��������ã� �������...
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
�� ��
��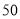 ����Ȼ���������£�
����Ȼ���������£�
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
����������������Ȧ��һ�����������ڵ�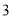 �������Ͳ������ǣ� ����
�������Ͳ������ǣ� ����
A. 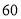 B.
B. 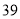 C.
C. 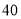 D.
D. 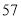

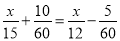 B.
B. 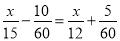
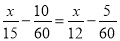 D.
D.