题目内容
对于任意实数x，多项式x2﹣5x+8的值是一个( )
A．非负数 B．正数 C．负数 D．无法确定
B【考点】配方法的应用；非负数的性质：偶次方．
【分析】根据完全平方公式，将x2﹣5x+8转化为完全平方的形式，再进一步判断．
【解答】解：x2﹣5x+8=x2﹣5x+
+
=（x﹣
）2+，
任意实数的平方都是非负数，其最小值是0，
所以（x﹣）2+的最小值是，
故多项式x2﹣5x+8的值是一个正数，
故选：B．
【点评】本题考查了配方法的应用和非负数的性质．任意实数的平方和绝对值都具有非负性，灵活运用这一性质是解决此类问题的关键．
练习册系列答案
相关题目
。
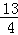，y1），B（
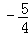，y2），C（
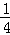，y3）为二次函数y=x2+4x﹣5的图象上的三点，则y1，y2，y3的大小关系是( )
_______．