题目内容
20.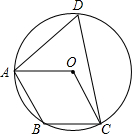 如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=( )
如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
分析 利用四边形OABC为平行四边形,可得∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.利用四边形ABCD是圆的内接四边形,可得∠D+∠B=180°.利用同弧所对的圆周角和圆心角可得∠D=$\frac{1}{2}$∠AOC,求出∠D=60°,进而即可得出.
解答 解:∵四边形OABC为平行四边形,
∴∠AOC=∠B,∠OAB=∠OCB,∠OAB+∠B=180°.
∵四边形ABCD是圆的内接四边形,
∴∠D+∠B=180°.
又∠D=$\frac{1}{2}$∠AOC,
∴3∠D=180°,
解得∠D=60°.
∴∠OAB=∠OCB=180°-∠B=60°.
∴∠OAD+∠OCD=360°-(∠D+∠B+∠OAB+∠OCB)=360°-(60°+120°+60°+60°)=60°.
故选B.
点评 本题考查了平行四边形的性质、圆的内接四边形的性质、同弧所对的圆周角和圆心角的关系,属于基础题.

练习册系列答案
相关题目
11.化简$\frac{1}{x-1}$+$\frac{2}{1-{x}^{2}}$结果是( )
| A. | x-1 | B. | x+1 | C. | $\frac{x+3}{{x}^{2}-1}$ | D. | $\frac{1}{x+1}$ |
15.用描点法画二次函数y=-x2-2x+1的图象.
(1)列表:
在下列平面直角坐标系中描出表中各点,并把这些点连成平滑的曲线;

(2)若作其图象关于y轴的对称图形,求所得图象对应的表达式.
(1)列表:
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y=-x2-2x+1 | … | -2 | 1 | 2 | 1 | -2 |

(2)若作其图象关于y轴的对称图形,求所得图象对应的表达式.
9.已知等腰三角形的一个内角是70°,则这个等腰三角形的顶角为( )
| A. | 70° | B. | 40° | C. | 70°或40° | D. | 以上答案都不对 |
