题目内容
下列说法错误的是（ ）
| A、对角线相等是矩形具有而菱形不具有的性质 |
| B、对角线互相垂直平分是正方形具有而菱形不具有的性质 |
| C、每一条对角线平分一组对角是菱形具有而矩形不具有的性质 |
| D、顺次连接任意四边形各边中点所得的四边形一定是平行四边形 |
考点：中点四边形,菱形的性质,矩形的性质,正方形的性质
专题：
分析：利用中点四边形及特殊的平行四边形的判定方法逐一判断后即可确定正确的选项．
解答：解：A、对角线相等是矩形具有而菱形不具有的性质，正确；
B、菱形的对角线也互相垂直平分，故错误；
C、每一条对角线平分一组对角是菱形具有而矩形不具有的性质，正确；
D、顺次连接任意四边形各边中所得的四边形一定是平行四边形，正确，
故选B．
B、菱形的对角线也互相垂直平分，故错误；
C、每一条对角线平分一组对角是菱形具有而矩形不具有的性质，正确；
D、顺次连接任意四边形各边中所得的四边形一定是平行四边形，正确，
故选B．
点评：本题考查了中点四边形及特殊的平行四边形的判定方法，牢记这些判定方法是解答本题的关键．
练习册系列答案
相关题目
列方程（组）解应用题：
如图，△ABC内接于⊙O，DA切⊙O于点A，交BC的延长线于点D．若∠B=25°，∠ACB=80°，则∠D的度数为
如图，点O在Rt△ABC的斜边AB上，⊙O切AC边于点E，切BC边于点D，连结OE，如果由线段CD、CE及劣弧ED围成的图形（阴影部分）面积与△AOE的面积相等，那么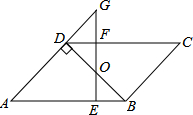
如图，?ABCD中，BD⊥AD，∠A=45°，E、F分别是AB，CD上的点，且BE=DF，连接EF交BD于O．
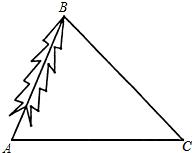为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求这棵古杉树AB的长度．（结果取整数）