题目内容
8.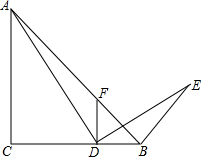 如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.
如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.(1)求证:AB⊥BE;
(2)若AC=8,DF=3,求BE的长.
分析 (1)作EH⊥BC于H,如图,根据旋转的性质得∠ADE=90°,DA=DE,再利用等角的余角相等得到∠EDH=∠DAC,则可根据“AAS”证明△ACD≌△DHE得到AC=DH,CD=EH,接着利用∠C=90°,AC=BC和等线段代换可得BH=EH,于是可判断△BEH为等腰直角三角形,所以∠EBH=45°,则可得到∠ABE=90°,然后根据垂直的定义得AB⊥BE;
(2)由于DF⊥BC,∠FBD=45°,则可判断△DBF为等腰直角三角形,得到BD=DF=3,再利用BC=AC=8得到CD=5,然后利用(1)中的证明过程得EH=CD=5,△BEH为等腰直角三角形,于是BE=$\sqrt{2}$EH=5$\sqrt{2}$.
解答 (1)证明:作EH⊥BC于H,如图,
∵AD绕点D顺时针旋转90°得到DE,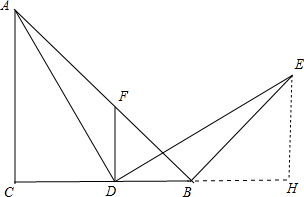
∴∠ADE=90°,DA=DE,
∴∠ADC+∠EDH=90°,
而∠ADC+∠DAC=90°,
∴∠EDH=∠DAC,
在△ACD和△DHE中
$\left\{\begin{array}{l}{∠C=∠H}\\{∠DAC=∠EDH}\\{AD=DE}\end{array}\right.$,
∴△ACD≌△DHE,
∴AC=DH,CD=EH,
∵∠C=90°,AC=BC,
∴∠ABC=45°,
∵AC=BC=DH,
∴CD=BH,
∴BH=EH,
∴△BEH为等腰直角三角形,
∴∠EBH=45°,
∴∠ABE=90°,
∴AB⊥BE;
(2)解:∵DF⊥BC,∠FBD=45°,
∴△DBF为等腰直角三角形,
∴BD=DF=3,
∵BC=AC=8,
∴CD=5,
由(1)得EH=CD=5,△BEH为等腰直角三角形,
∴BE=$\sqrt{2}$EH=5$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和等腰直角三角形的判定与性质.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | 2 | B. | -4 | C. | 2或-4 | D. | 无法确定 |
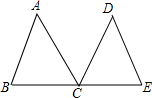 如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC.
如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC. 如图,有一斜坡AB长170m,坡顶离地面的高度BC为80m,求此斜坡的水平距离AC的长度.
如图,有一斜坡AB长170m,坡顶离地面的高度BC为80m,求此斜坡的水平距离AC的长度.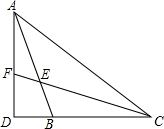 如图,在△ABC中,∠BAC=30°,∠ABC=110°,AD是BC边上的高,∠ACB的平分线交AB于点E,交AD于点F,试求∠AFC的度数.
如图,在△ABC中,∠BAC=30°,∠ABC=110°,AD是BC边上的高,∠ACB的平分线交AB于点E,交AD于点F,试求∠AFC的度数.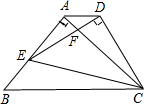 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤. 如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.