题目内容
9.学校校办厂需制作一块广告牌,请来两名工人,已知师傅单独完成需要4天,徒弟单独完成需要6天.(1)徒弟先做一天,再两人合作.共得报酬450元,按各人完成的工作量计算报酬,师徒各得多少?
(2)两人合作完成后共得报酬450元,工作量相同部分的报酬,师徒按3:2分配,多出的部分按每人单独完成工作量的比例进行分配,师徒各得多少元?
分析 根据师徒单独制作时间可知,师傅一天可以完成广告牌的$\frac{1}{4}$,徒弟一天可以完成广告牌的$\frac{1}{6}$.
(1)设师傅工作了x天,则徒弟工作了(x+1)天,根据总工作量=徒弟完成的工作量+师傅完成的工作量即可得出关于x的一元一次方程,解之即可得出x的值,再根据报酬的分配方式为按各人完成的工作量计算,即可求出师徒各得多少钱;
(2)根据工作时间=工作总量÷工作效率即可求出制作广告牌需要的时间,结合两人的工作效率即可求出各自完成的工作量,再根据报酬的分配方式即可求出师徒各自获得的报酬,此题得解.
解答 解:根据师徒单独制作时间可知,师傅一天可以完成广告牌的$\frac{1}{4}$,徒弟一天可以完成广告牌的$\frac{1}{6}$.
(1)设师傅工作了x天,则徒弟工作了(x+1)天,
根据题意,得:$\frac{1}{4}$x+$\frac{1}{6}$(x+1)=1,
解得:x=2.
师傅获得的报酬为$\frac{1}{4}$×2×450=225(元),
徒弟获得的报酬为450-225=225(元).
答:师傅获得的报酬为225元,徒弟获得的报酬为225元.
(2)师徒二人共同工作的时间为:1÷($\frac{1}{4}$+$\frac{1}{6}$)=$\frac{12}{5}$(天),
徒弟完成了广告牌的$\frac{1}{6}$×$\frac{12}{5}$=$\frac{2}{5}$,
师傅完成了广告牌的$\frac{1}{4}$×$\frac{12}{5}$=$\frac{3}{5}$,
师徒完成工作量相同的部分占广告牌的$\frac{2}{5}$×2=$\frac{4}{5}$,
徒弟获得的报酬为:450×$\frac{4}{5}$×$\frac{2}{3+2}$=144(元),
师傅获得的报酬为:450-144=306(元).
答:师傅获得的报酬为306元,徒弟获得的报酬为144元.
点评 本题考查了一元一次方程的应用,根据数量关系列出一元一次方程(或列式计算)是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{x}{70}$-$\frac{x}{60}$=1 | B. | $\frac{x}{60}$-$\frac{x}{70}$=1 | C. | 70x-60x=1 | D. | $\frac{70}{x}$-$\frac{60}{x}$=1 |
| A. | 5 | B. | $\sqrt{97}$ | C. | 5 或$\sqrt{7}$ | D. | $\sqrt{97}$或$\sqrt{65}$ |
| A. | x3•x2=x5 | B. | (x3)2=x5 | C. | (x2y)2=x4y2 | D. | x5÷x2=x3 |
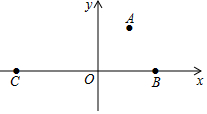 已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点.
已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点. 如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.
如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上. 如图,将一块含30°角的直角三角板的直角顶点放在相互平行的两条直线中的一条直线上,若∠1-∠2=18°,则∠3=24°.
如图,将一块含30°角的直角三角板的直角顶点放在相互平行的两条直线中的一条直线上,若∠1-∠2=18°,则∠3=24°.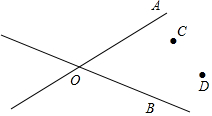 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)