题目内容
17. 将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N,若AB=4,AD=8,则线段AN的长为( )
将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N,若AB=4,AD=8,则线段AN的长为( )| A. | 8 | B. | 12 | C. | 5 | D. | 4 |
分析 由折叠得到AM=CM,设CM=x,则BM=8-x,关键勾股定理求出x,再判断四边形AMCN是平行四边形,即可.
解答  解:在矩形纸片ABCD中,AB=4,AD=8,
解:在矩形纸片ABCD中,AB=4,AD=8,
∴∠B=∠D,AD∥BC,BC=8,
由折叠得,AM=CM,
设CM=x,则BM=8-x,
在RT△ABM中,AM2=AB2+BM2,
即x2=16+(8-x)2,
∴x=5,
∴CM=5,
由折叠得,AM∥NC,
∵AD∥BC,
∴四边形AMCN是平行四边形,
∴AN=CM=5,
故选C,
点评 此题是折叠问题,考查了矩形的性质、折叠的性质、勾股定理以及平行四边形的性质和判定.用勾股定理求出CM是解本题的关键;此题难度适中,掌握数形结合思想与方程思想的应用.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
5.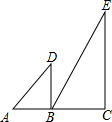 如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )
如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )
 如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )
如图,在直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°,若将△ABD绕点B按顺时针方向旋转,当AD∥BC时,旋转的角度是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.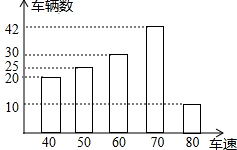 为了解一段路车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速((单位:千米/时),并绘制成如图所示的条形统计图,这些车速的众数、中位数分别是( )
为了解一段路车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速((单位:千米/时),并绘制成如图所示的条形统计图,这些车速的众数、中位数分别是( )
 为了解一段路车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速((单位:千米/时),并绘制成如图所示的条形统计图,这些车速的众数、中位数分别是( )
为了解一段路车辆行驶速度的情况,交警统计了该路段上午7:00至9:00来往车辆的车速((单位:千米/时),并绘制成如图所示的条形统计图,这些车速的众数、中位数分别是( )| A. | 80,60 | B. | 70,70 | C. | 60,60 | D. | 70,60 |
2.代数式$\sqrt{1-x}$有意义,则x的取值范围是( )
| A. | x>1,且x≠0 | B. | x≥1 | C. | x≠1 | D. | x≤1 |
9. 如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长等于( )
如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长等于( )
 如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长等于( )
如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长等于( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
7. 下列四个水平放置的几何体中,三视图如图所示的是( )
下列四个水平放置的几何体中,三视图如图所示的是( )
 下列四个水平放置的几何体中,三视图如图所示的是( )
下列四个水平放置的几何体中,三视图如图所示的是( )| A. |  立方体 | B. |  三棱柱 | C. |  圆柱 | D. |  长方体 |
 如图,在正方形ABCD中,点E、F分别在BC、CD上,且BE=DF,若∠EAF=30°,则sin∠EDF=$\frac{(\sqrt{3}-1)\sqrt{7+2\sqrt{3}}}{\sqrt{37}}$.
如图,在正方形ABCD中,点E、F分别在BC、CD上,且BE=DF,若∠EAF=30°,则sin∠EDF=$\frac{(\sqrt{3}-1)\sqrt{7+2\sqrt{3}}}{\sqrt{37}}$.