题目内容
11．
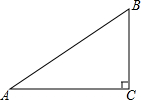如图，在Rt△ABC中，∠C=90°，∠B=60°，AB=8，求AC的长．
分析 在RT△ABC中，利用直角三角形的性质，结合已知条件易求∠A=30°，进而再利用30°的角所对的直角边等于斜边的一半，易求BC，再利用勾股定理可求AC．
解答 解：如右图所示，
在RT△ABC中，∠C=90°，∠B=60°，
∴∠A=30°，
又∵AB=8，
∴BC=4，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4$\sqrt{3}$．
点评 本题考查了含30°角的直角三角形的性质、勾股定理的运用，解题的关键是先求出BC．
练习册系列答案
相关题目
16．下列二元一次方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ |
20．
如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于$\frac{1}{2}$AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论不一定正确的是（ ）
如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于$\frac{1}{2}$AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论不一定正确的是（ ）| A． | AD=BD | B． | BD=CD | C． | ∠A=∠BED | D． | ∠ECD=∠EDC |